
【题目】如图,正方形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 两点同时出发,以
两点同时出发,以![]() 的速度沿
的速度沿![]() ,
,![]() 运动,到点
运动,到点![]() ,
,![]() 时停止运动,设运动时间为
时停止运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A.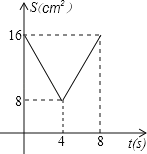 B.
B.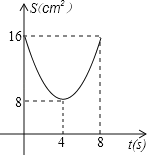 C.
C.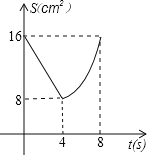 D.
D.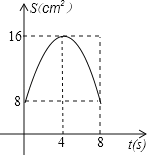
【答案】B
【解析】
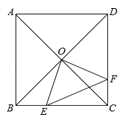
由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8﹣t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF,这样S四边形OECF=S△OBC=16,于是S=S四边形OECF﹣S△CEF=16﹣![]() (8﹣t)t,然后配方得到S=
(8﹣t)t,然后配方得到S=![]() (t﹣4)2+8(0≤t≤8),最后利用解析式和二次函数的性质即可得出结论.
(t﹣4)2+8(0≤t≤8),最后利用解析式和二次函数的性质即可得出结论.
根据题意得:BE=CF=t,CE=8﹣t.
∵四边形ABCD为正方形,∴OB=OC,∠OBC=∠OCD=45°.
在△OBE和△OCF中,∵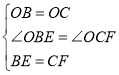 ,∴△OBE≌△OCF(SAS),∴S△OBE=S△OCF,∴S四边形OECF=S△OBC=
,∴△OBE≌△OCF(SAS),∴S△OBE=S△OCF,∴S四边形OECF=S△OBC=![]() ×82=16,∴S=S四边形OECF﹣S△CEF=16﹣
×82=16,∴S=S四边形OECF﹣S△CEF=16﹣![]() (8﹣t)t=
(8﹣t)t=![]() t2﹣4t+16=
t2﹣4t+16=![]() (t﹣4)2+8(0≤t≤8),∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.
(t﹣4)2+8(0≤t≤8),∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.
故选B.


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
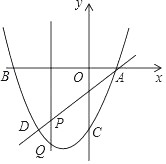
【题目】如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P是线段AD上的动点.
(1)b= ,抛物线的顶点坐标为 ;
(2)求直线AD的解析式;
(3)过点P的直线垂直于x轴,交抛物线于点Q,连接AQ,DQ,当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(﹣3,0),(0,﹣3).
(1)求抛物线的表达式.
(2)已知点(m,k)和点(n,k)在此抛物线上,其中m≠n,请判断关于t的方程t2+mt+n=0是否有实数根,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).

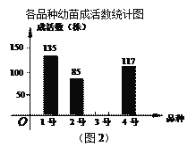
(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com