Question

15．如图所示，为了测量某段河面的宽度，李明同学设计了如下测量方案：同学在点A处观测对岸C点，测得∠CAD=45°，又在距A处120m远的B处测得∠CBA=30°，请你根据这些数据算出河宽约为多少？（精确到0.01m，参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）

Answer 1

分析 如图所示，CE即为所求线段，而在三角形ACE中，由于∠CAE=45°，则CE=AE，若假设CE=AE=x，则BE=120+x，所以在三角形BCE中tan30°=$\frac{EC}{EB}$，由此可以得到关于x的方程，然后解方程即可．

解答 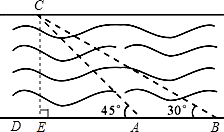解：过点C作CE⊥BA延长线于点E，
由题意可得：EC=AE，设EC=x，
则tan30°=$\frac{EC}{BE}$=$\frac{x}{x+120}$=$\frac{\sqrt{3}}{3}$，
解得：x=60（$\sqrt{3}$+1），
则EC=60（$\sqrt{3}$+1）≈163.92（m）．
答：河宽约为163.92m．

点评 此题主要考查了三角函数的概念和应用，解题关键是把实际问题转化为数学问题，抽象到三角形中，利用三角函数进行解答．