
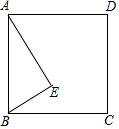
 如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.
如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.分析 (1)连接AC和BD,根据中心对称的性质可判断它们的交点为旋转中心O,延长EO到F,使FO=EO,则△CDF满足条件;
(2)过点O作OG⊥OE与EB的延长线交于点G,如图,先利用勾股定理计算出BE=6,再利用正方形的性质得OA=OB,∠AOB=90°,则∠AOE=∠BOG,接着根据三角形内角和得到∠GBO=∠EAO,于是可判断△EAO≌△GBO,所以AE=BG=8,OE=OG,然后判断△GEO为等腰直角三角形,则可得到OE=$\frac{\sqrt{2}}{2}$EG=$\frac{\sqrt{2}}{2}$(BG-BE)=$\sqrt{2}$,从而得到EF=2$\sqrt{2}$.
解答 解:(1)连接AC和BD,则它们的交点为旋转中心O,延长EO到F,使FO=EO,
如图,点O和△CDF为所作;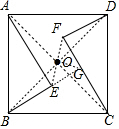 (2)过点O作OG⊥OE与EB的延长线交于点G,如图,
(2)过点O作OG⊥OE与EB的延长线交于点G,如图,
在Rt△ABE中,BE=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵四边形ABCD为正方形,
∴OA=OB,∠AOB=90°,
而∠EOG=90°,
∴∠AOE=∠BOG,
∵∠AEB=∠AOB=90°,
∴∠GBO=∠EAO,
∴在△EAO和△GBO中,
$\left\{\begin{array}{l}{∠EAO=∠GBO}\\{OA=OB}\\{∠AOE=∠BOG}\end{array}\right.$
∴△EAO≌△GBO,
∴AE=BG=8,OE=OG,
∴△GEO为等腰直角三角形,
∴OE=$\frac{\sqrt{2}}{2}$EG=$\frac{\sqrt{2}}{2}$(BG-BE)=$\frac{\sqrt{2}}{2}$×(8-6)=$\sqrt{2}$,
∴EF=2OE=2$\sqrt{2}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了正方形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A(-4,$\frac{1}{2}$)、B(-1,2)是反比例函数y=$\frac{a}{x}$与一次函数y=kx+b的图象在第二象限内的两个交点,AM⊥x轴于M,BN⊥y轴于N,
如图,A(-4,$\frac{1}{2}$)、B(-1,2)是反比例函数y=$\frac{a}{x}$与一次函数y=kx+b的图象在第二象限内的两个交点,AM⊥x轴于M,BN⊥y轴于N,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com