
【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣ ![]() ;⑤2a<b+
;⑤2a<b+ ![]() ,正确的是( )
,正确的是( )
A.①③
B.①②③
C.①②③⑤
D.①③④⑤
【答案】D
【解析】解:∵抛物线与x轴的交点为(1,0)和(x1 , 0),﹣2<x1<﹣1,与y轴交于正半轴, ∴a<0,
∵﹣2<x1<﹣1,
∴﹣ ![]() <﹣
<﹣ ![]() <0,
<0,
∴b<0,b>a,故①正确,②错误;
∵当x=﹣1时,y>0,
∴a﹣b+1>0,
∴a>b﹣1故③正确;
∵由一元二次方程根与系数的关系知x1x2= ![]() ,
,
∴x1= ![]() ,
,
∵﹣2<x1<﹣1,
∴﹣2< ![]() <﹣1,
<﹣1,
∴a<﹣ ![]() ,故④正确;
,故④正确;
∵当x=﹣2时,y<0,
∴4a﹣2b+1<0,
∴2a<b+ ![]() ,故⑤正确,
,故⑤正确,
综上所述,正确的结论有①③④⑤,
故选:D.
求得与y轴的交点坐标,根据与坐标轴的交点判断出a<0,根据与x轴的交点判定﹣ ![]() <﹣
<﹣ ![]() <0,从而得出a、b的关系,把(﹣1,0),(﹣2,0)代入函数解析式求出a、b、c的关系式,然后对各小题分析判断即可得解.
<0,从而得出a、b的关系,把(﹣1,0),(﹣2,0)代入函数解析式求出a、b、c的关系式,然后对各小题分析判断即可得解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为28块时,白色瓷砖块数为( )

A. 27 B. 28 C. 33 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
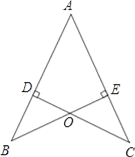
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+1与y轴交于A点,过点A的抛物线y=﹣
x+1与y轴交于A点,过点A的抛物线y=﹣ ![]() x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).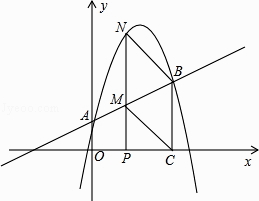
(1)直接写出抛物线的解析式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( ) 
A.94分,96分
B.96分,96分
C.94分,96.4分
D.96分,96.4分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com