练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平行四边形ABCD中，E、F分别是边BC、AD上的点，有下列条件：

    ①AE∥CF；②BE＝FD；③∠1＝∠2；④AE＝CF.

    若要添加其中一个条件，使四边形AECF一定是平行四边形，则添加的条件可以是(　 　)

    A. ①②③④ B. ①②③ C. ②③④ D. ①③④

    【答案】B

    【解析】

    由四边形ABCD是平行四边形，可得AD∥BC，AD=BC，∠BAD=∠BCD，然后利用平行四边形的判定分别分析求解，即可求得答案；注意利用举反例的方法可排除错误答案．

    ∵四边形ABCD是平行四边形，

    ∴AD∥BC，AD=BC，∠BAD=∠BCD，

    ∴当①AE∥CF时，四边形AECF是平行四边形；故①正确；

    当②BE=FD时，CE=AF，则四边形AECF是平行四边形；故②正确；

    当③∠1=∠2时，∠EAF=∠ECF，

    ∵∠EAF+∠AEC=180,∠AFC+∠ECF=180，

    ∴∠AFC=∠AEC，

    ∴四边形AECF是平行四边形；故③正确；

    ④若AE=AF，则四边形AECF是平行四边形或等腰梯形，故④错误.

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，P为AD边上一点，沿直线BP将△ABP翻折至△EBP（点A的对应点为点E），PE与CD相交于点O，且OE=OD．

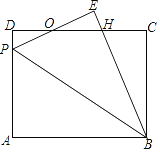
    （1）求证：PE=DH；

    （2）若AB=10，BC=8，求DP的长．

    【答案】（1）见解析；（2）．

    【解析】试题分析：(1) 先证明△DOP≌△EOH，再利用等量代换得到PE=DH.

    (2) 设DP=x， Rt△BCH中，先用 x表示三角形三边，利用勾股定理列式解方程.

    试题解析：

    （1）解：证明：∵OD=OE，∠D=∠E=90°，∠DOP=∠EOH，

    ∴△DOP≌△EOH，

    ∴OP=OH，

    ∴PO+OE=OH+OD，

    ∴PE=DH.

    （2）解：设DP=x，则EH=x，BH=10﹣x，

    CH=CD﹣DH=CD﹣PE=10﹣（8﹣x）=2+x，

    ∴在Rt△BCH中，BC2+CH2=BH2

    （2+x）2+82=（10﹣x）2，

    ∴x=,

    ∴DP=．

    【题型】解答题
    【结束】
    25

    【题目】某文教店老板到批发市场选购A，B两种品牌的绘图工具套装，每套A品牌套装进价比B品牌每套套装进价多2.5元，已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍．

    （1）求A，B两种品牌套装每套进价分别为多少元？

    （2）若A品牌套装每套售价为13元，B品牌套装每套售价为9.5元，店老板决定，购进B品牌的数量比购进A品牌的数量的2倍还多4套，两种工具套装全部售出后，要使总的获利超过120元，则最少购进A品牌工具套装多少套？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】与在平面直角坐标系中的位置如图所示．

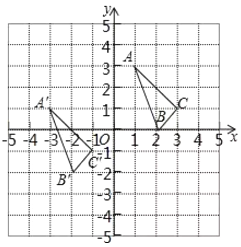
    （1）分别写出各点的坐标：___________，_________，_______________．

    （2）是由经过怎样的平移变换得到的？答：___________________．

    （3）若点是内部一点，则内部的对应点的坐标为___________．

    （4）求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“低碳环保，绿色出行”的概念得到广大群众的接受，越来越多的人喜欢选择骑自行车作为出行工具．小军和爸爸同时骑车去图书馆，爸爸先以150米/分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆．小军始终以同一速度骑行，两人骑行的路程为y(米)与时间x(分钟)的关系如图．请结合图象，解答下列问题：

    (1)填空：a=________；b=________；m=________．

    (2)若小军的速度是 120 米/分，求小军第二次与爸爸相遇时距图书馆的距离．

    (3)在(2)的条件下，爸爸自第二次出发后，骑行一段时间后与小军相距100 米，此时 小军骑行的时间为________分钟．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图①，已知直线l1∥l2，且l3和l1，l2分别交于A，B两点，点P在线段AB上，则∠1，∠2，∠3之间的等量关系是____；

    (2)如图②，点A在B处北偏东40°方向，在C处北偏西45°方向，则∠BAC＝____°.

    (3)如图③，∠ABD和∠BDC的平分线交于点E，BE交AB于点F，∠1＋∠2＝90°，试说明：AB∥AB，并探究∠2与∠3的数量关系．

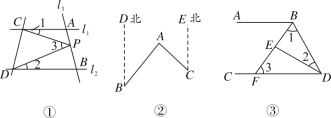
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2017次运动后，动点P的坐标是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．

    （1）在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，则D点的坐标；E点的坐标 ．
    （2）如图②，若AE上有一动点P（不与A、E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．求四边形PMNE的面积S与时间t之间的函数关系式；t取何值时，S有最大值，最大值是多少？
    （3）在（2）的条件下，当t为何值时，以A、M、E为顶点的三角形为等腰三角形，并求出相应时刻点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

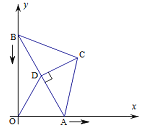
    【题目】如图，在△ABC中，BC＝AC＝5，AB＝8，CD为AB边的高，点A在x轴上，点B在y轴上，点C在第一象限，若A从原点出发，沿x轴向右以每秒4个单位长的速度运动，则点B随之沿y轴下滑，并带动△ABC在平面内滑动，设运动时间为t秒，当B到达原点时停止运动.当△ABC的边与坐标轴平行时，t＝_____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，对角线AC、BD相交于点O，AB⊥AC，AB＝3cm，BC＝5cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s.连结PO并延长交BC于点Q，设运动时间为t(0＜t＜5)．

    (1)当t为何值时，四边形ABQP是平行四边形？

    (2)设四边形OQCD的面积为y(cm2)，求y与t之间的函数关系式；

    (3)是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．

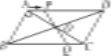
    　　备用图

    查看答案和解析>>

    同步练习册答案