
| A. | ①②⑤ | B. | ②③④ | C. | ①④⑤ | D. | ②④ |
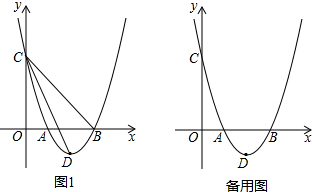
分析 令y=x2-kx+k-1=0,求出根的判别式即可判断①;当x=1时,y=0,抛物线总是经过一个定点(1,0),判断②正确;令k=4时,求出AB的长,判断③;求出y=x2-kx+k-1=0顶点坐标,然后代入y=-(x-1)2,进而作出判断;令k=1,得到y=x2-x,此时△ABC不是等腰三角形,据此作出判断.
解答 解:令y=x2-kx+k-1=0,
△=k2-4k+4=(k+2)2≥0,
即抛物线交x轴有两个的交点,①错误;
当x=1时,y=1-k+k-1=0,
即抛物线总是经过一个定点(1,0),②正确;
当k=4时,y=x2-4x+3,
令y=x2-4x+3=0,
解得x=3或1,
则AB=3-1=2,③错误;
y=x2-kx+k-1=0顶点坐标为($\frac{k}{2}$,$\frac{4k-{k}^{2}-4}{4}$),
当x=$\frac{k}{2}$时,y=-(x-1)2=-$\frac{{k}^{2}+4-4k}{4}$,
即抛物线的顶点在y=-(x-1)2图象上,④正确;
当k=1时,y=x2-x,此时△ABC不是等腰三角形,⑤错误;
正确的有②④,
故选D.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是掌握二次函数的性质以及抛物线与坐标轴交点问题,此题难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
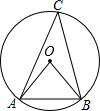 如图,圆O中,AO=5,弦AB长为8.C为弦AB所对优弧上的一点,求∠C的正切值( )
如图,圆O中,AO=5,弦AB长为8.C为弦AB所对优弧上的一点,求∠C的正切值( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
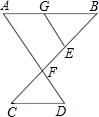 指出图中各对角的位置关系:
指出图中各对角的位置关系:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com