
【题目】在2019年春季环境整治活动中,某社区计划对面积为![]() 的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为
的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用5天.
区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成绿化任务,求
天,刚好完成绿化任务,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
【答案】(1)甲、乙两工程队每天能完成绿化面积分别为![]() 和
和![]() ;(2)
;(2)![]() ;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
【解析】
(1)设出两队的每天绿化的面积,以两队工作时间为等量构造分式方程;
(2)以(1)为基础表示甲乙两队分别工作x天、y天的工作总量,工作总量和为1600;
(3)用甲乙两队施工的总天数不超过25天确定自变量x取值范围,用x表示总施工费用,根据一次函数增减性求得最低费用.
解:(1)设乙工程队每天能完成绿化的面积为![]() ,
,
则甲工程队每天能完成绿化面积为![]() .
.
依题意得:![]() ,解得
,解得![]()
经检验:![]() 是原方程的根
是原方程的根
![]() .
.
答:甲、乙两工程队每天能完成绿化面积分别为![]() 和
和![]() .
.
(2)由(1)得:![]()
![]()
(3)由题意可知:![]()
即![]()
解得![]()
![]() 总费用
总费用![]()
![]() 值随
值随![]() 值的增大而增大.
值的增大而增大.
![]() 当
当![]() 天时,
天时,![]()
![]()
答:甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是( )
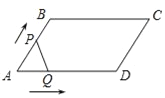
A. 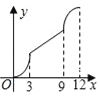 B.
B. 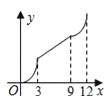 C.
C. 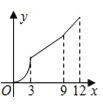 D.
D. 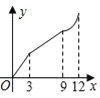
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在四个月的试销期内,只销售![]() 、
、![]() 两个品牌的电视机,共售出400台.如图1和图2为经销人员正在绘制的两幅统计图,请根据图中信息回答下列问题.
两个品牌的电视机,共售出400台.如图1和图2为经销人员正在绘制的两幅统计图,请根据图中信息回答下列问题.
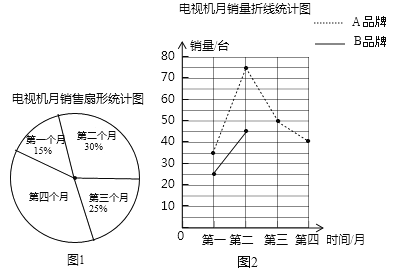
(1)第四个月两品牌电视机的销售量是多少台?
(2)先通过计算,再在图2中补全表示![]() 品牌电视机月销量的折线;
品牌电视机月销量的折线;
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,抽到![]() 品牌和抽到
品牌和抽到![]() 品牌电视机的可能性哪个大?请说明理由.
品牌电视机的可能性哪个大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的⊙O与AC相交于点D,过点D作DE⊥BC交AB延长线于点E,垂足为点F.
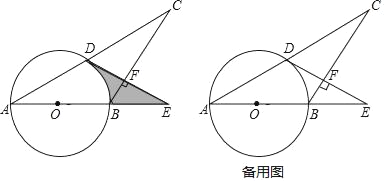
(1)证明:DE是⊙O的切线;
(2)若BE=4,∠E=30°,求由![]() 、线段BE和线段DE所围成图形(阴影部分)的面积,
、线段BE和线段DE所围成图形(阴影部分)的面积,
(3)若⊙O的半径r=5,sinA=![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,点
,点![]() ,
,![]() 在线段
在线段![]() 上且
上且![]() ;
;![]() 是线段
是线段![]() 上的动点,分别以
上的动点,分别以![]() ,
,![]() 为边在线段
为边在线段![]() 的同侧作等边
的同侧作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,设
,设![]() 的中点为
的中点为![]() ;当点
;当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 移动路径的长是( )
移动路径的长是( )
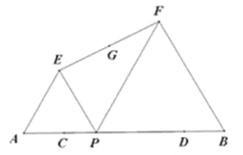
A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
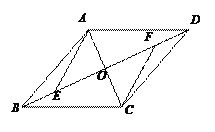
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文第一次刚好是花生馅粽的概率为____________.
(2)用树状图或列表的方法求出小文吃前两个粽子都是花生馅粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A﹣C﹣B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1,C2两段组成,如图2所示.
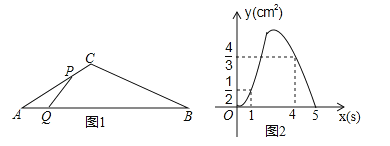
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
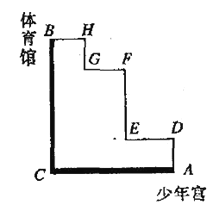
【题目】如图,粗线![]() 和细线
和细线![]() 是公交车从少年宫
是公交车从少年宫![]() 到体育馆
到体育馆![]() 的两条行驶路线.
的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆![]() 到少年宫
到少年宫![]() ,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费
,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费![]() 元与行驶路程
元与行驶路程![]() (
(![]() )千米之间的关系;
)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com