练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知，点，在线段上且；是线段上的动点，分别以，为边在线段的同侧作等边和等边，连接，设的中点为；当点从点运动到点时，则点移动路径的长是（ ）

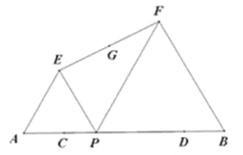
    A. 6B. 5C. 4D. 3

    【答案】D

    【解析】

    分别延长AE、BF交于点H，易证四边形EPFH为平行四边形，得出G为PH中点，则G的运行轨迹为三角形HCD的中位线MN．再求出CD的长，运用中位线的性质求出MN的长度即可．

    如图，分别延长AE、BF交于点H.

    ∵∠A=∠FPB=60°，

    ∴AH∥PF，

    ∵∠B=∠EPA=60°，

    ∴BH∥PE，

    ∴四边形EPFH为平行四边形，

    ∴EF与HP互相平分.

    ∵G为EF的中点，

    ∴G正好为PH中点，即在P的运动过程中，G始终为PH的中点，所以G的运行轨迹为三角形HCD的中位线MN.

    ∵CD=1022=6，

    ∴MN=3，即G的移动路径长为3.

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在综合与实践课上，老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.

    （1）奋进小组用图1中的矩形纸片ABCD，按照如图2所示的方式，将矩形纸片沿对角线AC折叠，使点B落在点处，则与重合部分的三角形的类型是________.

    （2）勤学小组将图2中的纸片展平，再次折叠，如图3，使点A与点C重合，折痕为EF，然后展平，则以点A、F、C、E为顶点的四边形是什么特殊四边形？请说明理由．

    （3）创新小组用图4中的矩形纸片ABCD进行操作，其中，，先沿对角线BD对折，点C落在点的位置，交AD于点G，再按照如图5所示的方式折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M．则EM的长为________cm.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在水平地面上有一幢房屋BC与一棵树DE，在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°，∠CAD=60°，在屋顶C处测得∠DCA=90°．若房屋的高BC=6米，则树高DE的长度为（　　）

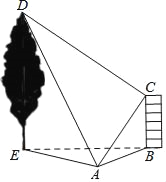
    A. 3 B. 6 C. 3 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：

    组别

    分数段（分）

    频数

    频率

    A组

    60≤x＜70

    30

    0.1

    B组

    70≤x＜80

    90

    n

    C组

    80≤x＜90

    m

    0.4

    D组

    90≤x＜100

    60

    0.2

    （1）在表中：m=　 　，n=　 　；

    （2）补全频数分布直方图；

    （3）4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．

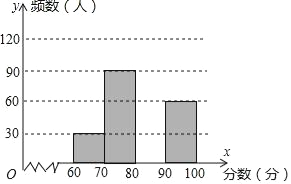
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一张正方形桌子可坐4人，按图1—图3的方式将桌子拼在一起并安排人员就坐．

    （1）两张桌子拼在一起可做 人，三张桌子拼在一起可坐 人，张桌子拼在一起可坐 人

    （2）一家酒楼有60张这样的桌子，按照图1—图3方式每4张拼成一个大桌子，则60张桌子可拼成15张大桌子，共可坐 人

    （3）在问题（2）中，若每4张桌子拼成一个大的正方形桌子，则可坐 人

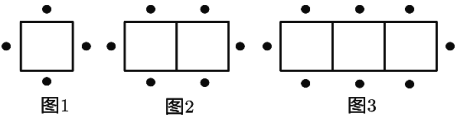
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在2019年春季环境整治活动中，某社区计划对面积为的区域进行绿化.经投标，由甲、乙两个工程队来完成，若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且在独立完成面积为区域的绿化时，甲队比乙队少用5天.

    （1）求甲、乙两工程队每天能完成绿化的面积；

    （2）设甲工程队施工天，乙工程队施工天，刚好完成绿化任务，求关于的函数关系式；

    （3）在（2）的条件下，若甲队每天绿化费用是0.6万元，乙队每天绿化费用为0.25万元，且甲乙两队施工的总天数不超过25天，则如何安排甲乙两队施工的天数，使施工总费用最低？并求出最低费用.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

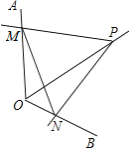
    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（　　）

    A. ∠BCA=∠F； B. ∠B=∠E； C. BC∥EF ； D. ∠A=∠EDF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠B＝90°，AC＝12，∠A＝60°．点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．

    （1）AB的长是　 　．

    （2）在D、E的运动过程中，线段EF与AD的关系是否发生变化？若不变化，那么线段EF与AD是何关系，并给予证明；若变化，请说明理由．

    （3）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．

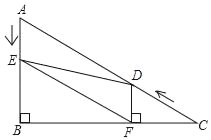
    查看答案和解析>>

    同步练习册答案