
【题目】如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,则树高DE的长度为( )
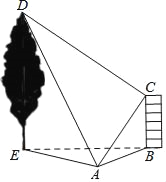
A. 3![]() B. 6
B. 6![]() C. 3
C. 3![]() D. 6
D. 6![]()
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
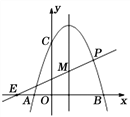
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴交于A(-1,0),B(3,0)两点,与
轴交于A(-1,0),B(3,0)两点,与![]() 轴交于点C(0,3),动点P在抛物线上,直线PE与抛物线的对称轴交于点M,点E的坐标为(-2,0).
轴交于点C(0,3),动点P在抛物线上,直线PE与抛物线的对称轴交于点M,点E的坐标为(-2,0).
(1)求抛物线的函数表达式;
(2)若P与C关于抛物线的对称轴对称,求直线PE的函数表达式;
(3)若PM=![]() EM,求点P的坐标.
EM,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
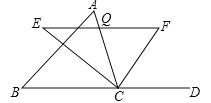
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查的样本为 ,样本容量为 ;
(2)在频数分布表中,组距为 ,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
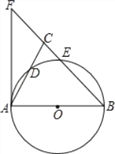
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在四个月的试销期内,只销售![]() 、
、![]() 两个品牌的电视机,共售出400台.如图1和图2为经销人员正在绘制的两幅统计图,请根据图中信息回答下列问题.
两个品牌的电视机,共售出400台.如图1和图2为经销人员正在绘制的两幅统计图,请根据图中信息回答下列问题.
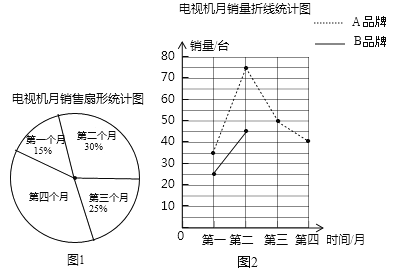
(1)第四个月两品牌电视机的销售量是多少台?
(2)先通过计算,再在图2中补全表示![]() 品牌电视机月销量的折线;
品牌电视机月销量的折线;
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,抽到![]() 品牌和抽到
品牌和抽到![]() 品牌电视机的可能性哪个大?请说明理由.
品牌电视机的可能性哪个大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五个城市的国际标准时间(单位:时)在数轴上表示如图所示.对应于北京时间2009年1月1日上午9时这一时刻,下列说法错误的是( ).

A.伦敦时间为2009年1月1日凌晨1时
B.纽约时间为2008年12月31日晚上20时
C.圣多明各时间为2008年12月31日晚上22时
D.首尔时间为2009年1月1日上午10时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,点
,点![]() ,
,![]() 在线段
在线段![]() 上且
上且![]() ;
;![]() 是线段
是线段![]() 上的动点,分别以
上的动点,分别以![]() ,
,![]() 为边在线段
为边在线段![]() 的同侧作等边
的同侧作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,设
,设![]() 的中点为
的中点为![]() ;当点
;当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 移动路径的长是( )
移动路径的长是( )
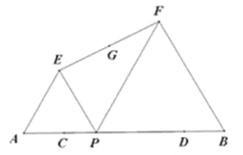
A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,若平移点
,若平移点![]() 到点
到点![]() ,使以点
,使以点![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )

A. 向左平移(![]() )个单位,再向上平移1个单位
)个单位,再向上平移1个单位
B. 向左平移![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
C. 向右平移![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com