
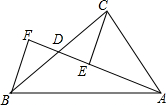
 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先利用SAS证明△BDF≌△CDE,再结合全等三角形的性质可得证②④,由于AD是△ABC的中线,由于等底同高,那么两个三角形的面积相等.
解答 解:①∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDF=∠CDE}\\{DF=DE}\end{array}\right.$,
∴△BDF≌△CDE;
②∵△BDF≌△CDE,
∴CE=BF;
③∵AD是△ABC的中线,
∴S△ABD=S△ACD.
④∵△BDF≌△CDE,
∴∠CED=∠BFD,
∴BF∥CE;
故选D.
点评 本题考查了全等三角形判定和性质,平行线的判定,三角形面积的计算,解题的关键是证明△BDF≌△CDE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
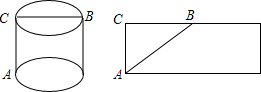 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:| A. | 楠楠同学正确,他的理论依据是“直线段最短” | |
| B. | 浩浩同学正确,他的理论依据是“两点确定一条直线” | |
| C. | 楠楠同学正确,他的理论依据是“垂线段最短” | |
| D. | 浩浩同学正确,他的理论依据是“两点之间,线段最短” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
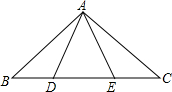 已知如图,在△ABC中,AB=AC,D、E是BC上异于B、C的任意两点,连接AD和AE,且AD=AE.
已知如图,在△ABC中,AB=AC,D、E是BC上异于B、C的任意两点,连接AD和AE,且AD=AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com