
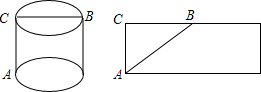
 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:| A. | 楠楠同学正确,他的理论依据是“直线段最短” | |
| B. | 浩浩同学正确,他的理论依据是“两点确定一条直线” | |
| C. | 楠楠同学正确,他的理论依据是“垂线段最短” | |
| D. | 浩浩同学正确,他的理论依据是“两点之间,线段最短” |
科目:初中数学 来源: 题型:填空题
 如图,菱形OABC在直角坐标系中,点A的坐标为($\frac{5}{2}$,0),对角线OB=$2\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)经过点C.则k的值为3.
如图,菱形OABC在直角坐标系中,点A的坐标为($\frac{5}{2}$,0),对角线OB=$2\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)经过点C.则k的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
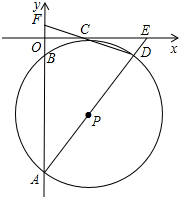 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,-1).
如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将一张矩形纸片ABCD沿着过点A的折痕翻折,使点B落在AD边上的点F,折痕交BC于点E,将折叠后的纸片再次沿着另一条过点A的折痕翻折,点E恰好与点D重合,此时折痕交DC于点G,则CG:GD的值为$\frac{\sqrt{2}}{2}$.
如图,将一张矩形纸片ABCD沿着过点A的折痕翻折,使点B落在AD边上的点F,折痕交BC于点E,将折叠后的纸片再次沿着另一条过点A的折痕翻折,点E恰好与点D重合,此时折痕交DC于点G,则CG:GD的值为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
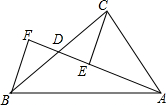 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,
在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com