
 在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,
在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,分析 (1)根据众数的定义即出现次数最多的数据进而得出即可,再利用中位数的定义得出即可;
(2)利用条形统计图得出各组频数,再根据加权平均数的公式计算即可;
(3)利用样本估计总体的思想,用总数乘以捐款平均数即可得到捐款总数.
解答 解:(1)数据15元出现了20次,出现次数最多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
故答案为15,15;
(2)50名同学捐款的平均数=(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
(3)估计这个中学的捐款总数=800×13=10400(元).
点评 此题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.除此之外,本题也考查了平均数、中位数、众数的定义以及利用样本估计总体的思想.


科目:初中数学 来源: 题型:选择题
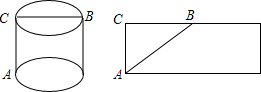 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:| A. | 楠楠同学正确,他的理论依据是“直线段最短” | |
| B. | 浩浩同学正确,他的理论依据是“两点确定一条直线” | |
| C. | 楠楠同学正确,他的理论依据是“垂线段最短” | |
| D. | 浩浩同学正确,他的理论依据是“两点之间,线段最短” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
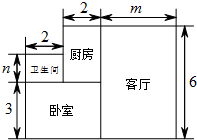 小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-3)2+2 | B. | y=(x-3)2-1 | C. | y=(x+3)2-1 | D. | y=(x-3)2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
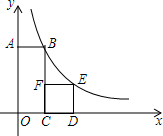 如图,点B、E在反比例函数y=$\frac{k}{x}$的图象上,矩形OABC的顶点A在y轴的正半轴上,正方形CDEF的顶点C、D在x轴的正半轴上,顶点F在BC上.若正方形CDEF的边长为2,且CB=3CF,则反比例函数的关系式为y=$\frac{6}{x}$.
如图,点B、E在反比例函数y=$\frac{k}{x}$的图象上,矩形OABC的顶点A在y轴的正半轴上,正方形CDEF的顶点C、D在x轴的正半轴上,顶点F在BC上.若正方形CDEF的边长为2,且CB=3CF,则反比例函数的关系式为y=$\frac{6}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com