
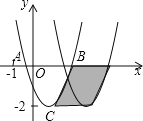
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线
与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线![]()
![]() ,则下列结论:①a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则
,则下列结论:①a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则![]() .其中正确的是_____(写出所有正确结论的序号)
.其中正确的是_____(写出所有正确结论的序号)
【答案】①③④
【解析】
①根据抛物线y=ax2+bx+c的图象,可得x=﹣1时,y>0,即a﹣b+c>0,据此判断即可;
②首先根据抛物线开口向上,可得a>0;然后根据对称轴为x![]() 0,可得b<0,据此判断即可;
0,可得b<0,据此判断即可;
③首先判断出阴影部分是一个平行四边形,然后根据平行四边形的面积=底×高,求出阴影部分的面积是多少即可;
④根据函数的最小值是![]() ,判断出c=﹣1时,a、b的关系即可.
,判断出c=﹣1时,a、b的关系即可.
∵x=﹣1时,y>0,∴a﹣b+c>0,∴结论①正确;
∵抛物线开口向上,∴a>0.
又∵对称轴为x![]() 0,∴b<0,∴结论②不正确;
0,∴b<0,∴结论②不正确;
∵抛物线向右平移了2个单位,∴平行四边形的底是2.
∵函数y=ax2+bx+c的最小值是y=﹣2,∴平行四边形的高是2,∴阴影部分的面积是:2×2=4,∴结论③正确;
∵![]() ,c=﹣1,∴b2=4a,∴结论④正确.
,c=﹣1,∴b2=4a,∴结论④正确.
综上,结论正确的是:①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
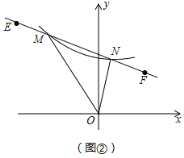
【题目】如图①,已知点A在反比例函数![]() (x>0)的图像上,点B在经过点(-2,1)的反比例函数
(x>0)的图像上,点B在经过点(-2,1)的反比例函数![]() (x<0)的图像上,连结OA,OB,AB.
(x<0)的图像上,连结OA,OB,AB.

(1)求k的值;
(2)若∠AOB=90°,求∠OAB的度数;
(3)将反比例函数![]() (x>0)的图像绕坐标原点O逆时针旋转45°得到曲线l,过点E
(x>0)的图像绕坐标原点O逆时针旋转45°得到曲线l,过点E![]() ,F
,F![]() 的直线与曲线l相交于点M,N,如图②所示,求△OMN的面积.
的直线与曲线l相交于点M,N,如图②所示,求△OMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,线段EF在对角线AC上(E不与A重合,F不与C重合),EG⊥AD,FH⊥BC,垂足分别是G、H,且EG+FH=EF.
(1)写出图中与△AEG相似的三角形;
(2)求线段EF的长;
(3)设EG=x,△AEG与△CFH的面积和为S,写出S关于x的函数关系式及自变量x的取值范围,并求出S的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:
在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有__________ ;
(2)性质探究:
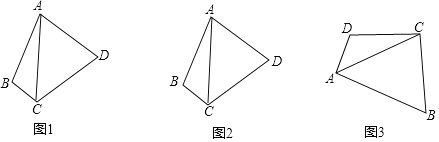
①如图1,四边形ABCD是奇异四边形,AB=AD,求证:CA平分∠BCD;
②如图2,四边形ABCD是奇异四边形,AB=AD,∠BCD=2α,试说明:cosα=![]() ;
;
(3)性质应用:
如图3,四边形ABCD是奇异四边形,四条边中仅有BC=CD,且四边形ABCD的周长为6+2![]() ,∠BAC=45°,AC=3
,∠BAC=45°,AC=3![]() ,求奇异四边形ABCD的面积.
,求奇异四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c的图象过点A(3,0),C(﹣1,0).
(1)求二次函数的解析式;
(2)如图,点P是二次函数图象的对称轴上的一个动点,二次函数的图象与y轴交于点B,当PB+PC最小时,求点P的坐标;
(3)在第一象限内的抛物线上有一点Q,当△QAB的面积最大时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF![]() DE.
DE.
(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD![]() 4,DE
4,DE![]() 5,求DM的长.
5,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在把一张正方形纸片按如图方式剪去一个半径为40![]() 厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,
厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

A. 64 B. 67 C. 70 D. 73
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com