
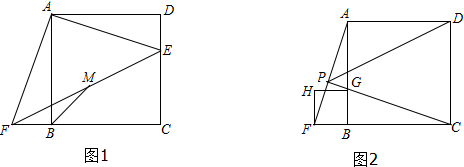
分析 (1)由四边形ABCD是正方形,得到AB=AD,∠ABC=∠BAD=∠D=90°,∠ABF=90°,因为∠FAE=90°,所以∠FAE-∠BAE=∠BAD-∠BAE,即;∠FAB=∠EAD,得到△ABF≌△DAE,求出AF=AE;
(2)取FC的中点N,连接MN,AM,因为点M是FE的中点,得到CE=2MN,由∠AKM=∠FKB,∠AMF=∠MNB=90°,得到△AKM~△BKM,$\frac{AK}{FK}$=$\frac{KM}{BK}$,因为∠AKB∠=MKB,所以△AFK∽△BKF,得到∠KBM=∠AFK=45°,∠MBN=45°,所以BM=$\sqrt{2}MN$,$\frac{BM}{CE}$=$\frac{\sqrt{2}}{2}$;
(3)过点D作DQ⊥PD交PC的延长线于Q,由四边形BFHG是正方形,得到BG=BF,所以△ABF≌△CBG,∠FAB=∠BCG,由∠AGP=∠CGB,得到∠APG=∠ABC=90°,因为∠ADC=∠PDQ=90°,得到∠ADP=∠QDC,由AB∥CD,得到∠DCQ=∠AGC,∠PAG+∠BAD=∠PAG+∠APG,即∠PAD=∠AGC=∠DCQ,得到△PAD≌△QCD(ASA),PD=DQ,∠DPQ=45°,得出∠APD=45°.
解答 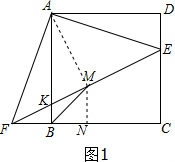 解:(1)如图1∵四边形ABCD是正方形,
解:(1)如图1∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠BAD=∠D=90°,
∴∠ABF=90°,
∵∠FAE=90°,∴∠FAE-∠BAE=∠BAD-∠BAE,
即;∠FAB=∠EAD,
在△ABF与△DAE中,
$\left\{\begin{array}{l}{∠ABF=DAE}\\{AB=AD}\\{∠ABF=∠D}\end{array}\right.$,
△ABF≌△DAE(ASA),
∴AF=AE;
(2)如图1取FC得中点N,连接MN,AM,
∵点M是FE的中点,
∴CE=2MN,
∵∠AKM=∠FKB,∠AMF=∠MNB=90°,
∴△AKM∽△BKF,
∴$\frac{AK}{FK}$=$\frac{KM}{BK}$,∵∠AKB∠=MKB,
∴△AFK∽△BKF,
∴∠KBM=∠AFK=45°,
∴∠MBN=45°,∴BM=$\sqrt{2}MN$,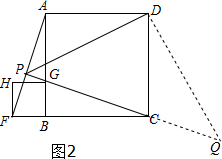
∴$\frac{BM}{CE}$=$\frac{\sqrt{2}}{2}$;
(3)如图2过点D作DQ⊥PD交PC的延长线于Q,
∵四边形BFHG是正方形,
∴BG=BF,
在△ABF与△CBG中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠ABC}\\{BF=BG}\end{array}\right.$,
∴△ABF≌△CBG(SAS),
∴∠FAB=∠BCG,
∵∠AGP=∠CGB,
∴∠APG=∠ABC=90°,
∵∠ADC=∠PDQ=90°,
∴∠ADP=∠QDC,
∵AB∥CD,∴∠DCQ=∠AGC,∴∠PAG+∠BAD=∠PAG+∠APG,
即∠PAD=∠AGC=∠DCQ,
在△PAD与△DCQ中,$\left\{\begin{array}{l}{∠PAD=∠QCD}\\{AD=CD}\\{∠ADP=∠QDC}\end{array}\right.$
∴△PAD≌△QCD(ASA),
∴PD=DQ,
∴∠DPQ=45°,
∴∠APD=45°.
故答案:45°.
点评 本题主要考查了正方形的性质、等腰直角三角形的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质等知识点,正确的做出辅助线是截图的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 1-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
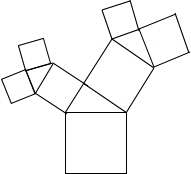 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.| A. | 28 | B. | 49 | C. | 98 | D. | 147 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
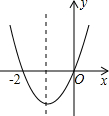 如图,根据二次函数y=ax2+bx+c(a≠0)的图象,有下列几种说法:
如图,根据二次函数y=ax2+bx+c(a≠0)的图象,有下列几种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com