
【题目】如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3).

(1)求b,c的值.
(2)P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当P(2,5)时,四边形APQO是平行四边形
;(2)当P(2,5)时,四边形APQO是平行四边形
【解析】
(1)根据题意得到点B的坐标,把A,B的坐标代入二次函数解析式,列出关于系数b、c的方程组,通过解方程组可以求得它们的值;
(2)由条件可知OA∥PQ,则PQ=3时,OAPQ为平行四边形,设P(m,-m2+3m+3),Q(m,m),可得关于m的方程,求出m的值即可求解.
解:(1)∵A(0,3),等腰Rt△OAB,
∴AB=3=OA,
∴B(3,3),
将点A、B的坐标代入y=﹣x2+bx+c得:
![]() ,
,
∴![]() ,
,
(2)存在,
∵B(3,3),
∴OB的解析式为y=x,
∵y=﹣x2+3x+3,
设P(m,﹣m2+3m+3),Q(m,m),
∵PQ⊥AB,OA⊥AB,
∴OA∥PQ,
若四边形APQO是平行四边形,
∴PQ=﹣m2+3m+3﹣m=3,
解得m=0(舍去),m=2,
当m=2时,y=﹣4+6+3=5,
∴p(2,5),
即当P(2,5)时,四边形APQO是平行四边形.
故答案为:(1)![]() ;(2)当P(2,5)时,四边形APQO是平行四边形.
;(2)当P(2,5)时,四边形APQO是平行四边形.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣bx.
(1)若此抛物线与直线y=x只有一个公共点,且向右平移1个单位长度后,刚好过点(3,0).
①求此抛物线的解析式;
②以y轴上的点P(0,n)为中心,作该抛物线关于点P对称的抛物线y',若这两条抛物线有公共点,求n的取值范围;
(2)若a>0,将此抛物线向上平移c个单位(c>0),当x=c时,y=0;当0<x<c时,y>0.试比较ac与1的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
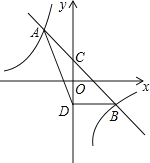
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C,BD垂直于y轴于点D.
的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C,BD垂直于y轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)求△ABD的面积;
(3)若M(x,y)、N(x,y)是反比例函数y=![]() 上的两点,当x<x<0时,直接写出y与y的大小关系
上的两点,当x<x<0时,直接写出y与y的大小关系
查看答案和解析>>
科目:初中数学 来源: 题型:
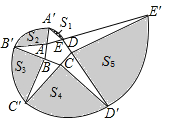
【题目】如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A′,再以点B为圆心,BA′为半径作圆弧交CB的延长线于B′,依次进行.得到螺旋线,再顺次连结EA′,AB′,BC′,CD′,DE′,得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
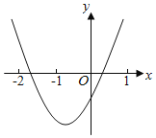
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
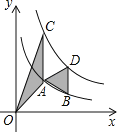
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“魅”、“力”、“宜”、“昌”的四个个球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“宜”的概率为多少?
(2)甲同学从中任取一球,记下汉字后放回袋中,然后再从袋中任取一球,请用画树图成列表的方法求出甲同学取出的两个球上的汉字恰能组成“魅力”或“宜昌”的概率p甲;
(3)乙同学从中任取一球,不放回,再从袋中任取一球,请求出乙同学取出的两个球上的汉字恰能组成“魅力”或“宜昌”的概率p乙,并指出p甲、p乙的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com