
【题目】如图一,抛物线![]() 过
过![]() 三点
三点
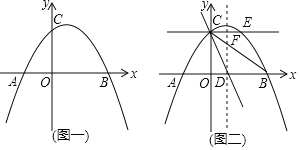
(1)求该抛物线的解析式;
(2)![]() 两点均在该抛物线上,若
两点均在该抛物线上,若![]() ,求
,求![]() 点横坐标
点横坐标![]() 的取值范围;
的取值范围;
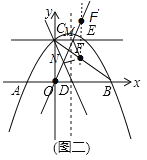
(3)如图二,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,该抛物线的对称轴与
,该抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 分别为直线
分别为直线![]() 和
和![]() 上的动点,求
上的动点,求![]() 周长的最小值.
周长的最小值.
【答案】(1)![]() ;(2)
;(2)![]() 点横坐标
点横坐标![]() 的取值范围:
的取值范围:![]() 或
或![]() ;(3)
;(3)![]() 的周长最小值为3.
的周长最小值为3.
【解析】
(1)将三个点的坐标代入,求出![]() ,即可求出关系式;
,即可求出关系式;
(2)可以求出点![]() 关于对称轴的对称点的横坐标为:
关于对称轴的对称点的横坐标为:![]() ,根据函数的增减性,可以求出当
,根据函数的增减性,可以求出当![]() 时
时![]() 点横坐标
点横坐标![]() 的取值范围;
的取值范围;
(3)由于点![]() 是
是![]() 的中点,可求出点
的中点,可求出点![]() 的坐标,根据对称找出
的坐标,根据对称找出![]() 关于直线
关于直线![]() 的对称点,连接两个对称点的直线与
的对称点,连接两个对称点的直线与![]() 的交点
的交点![]() ,此时三角形的周长最小,周长就等于这两个对称点之间的线段的长,根据坐标,和勾股定理可求.
,此时三角形的周长最小,周长就等于这两个对称点之间的线段的长,根据坐标,和勾股定理可求.
解:(1)∵抛物线![]() 过
过![]() 三点
三点
∴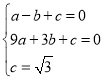 解得:
解得:![]() ;
;
∴抛物线的解析式为:![]() .
.
(2)抛物线的对称轴为![]() ,抛物线上与
,抛物线上与![]() 相对称的点
相对称的点![]()
![]() 在该抛物线上,
在该抛物线上,![]() ,根据抛物线的增减性得:
,根据抛物线的增减性得:
∴![]() 或
或![]()
答:![]() 点横坐标
点横坐标![]() 的取值范围:
的取值范围:![]() 或
或![]() .
.
(3)∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∵![]() 是
是![]() 的中点,
的中点,
∴![]()
当点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,关于直线
,关于直线![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与
与![]() 、
、![]() 交点为
交点为![]() ,此时
,此时![]() 的周长最小,周长为
的周长最小,周长为![]() 的长,由对称可得到:
的长,由对称可得到:![]() ,
,![]() 即点
即点![]() ,
,
 ,
,
即:![]() 的周长最小值为3,
的周长最小值为3,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
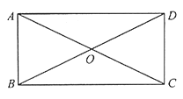
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CBA=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A. B两点,与y轴交于点D(0,6).
+bx+c经过A. B两点,与y轴交于点D(0,6).
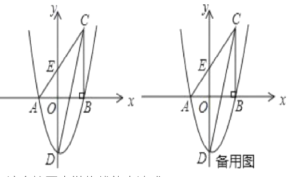
(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
(I).求抛物线的解析式及它的对称轴;
(Ⅱ)点![]() 在线段OB上,点Q在线段BC上,若
在线段OB上,点Q在线段BC上,若![]() ,且
,且![]() ,求n的值;
,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
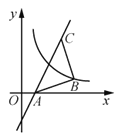
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程mx2+3x+1=0有两个不相等的实数根,则m的取值范围为( )
A. m<![]() B. m<
B. m<![]() 且m≠0C. m≤
且m≠0C. m≤![]() D. m≤
D. m≤![]() 且m≠0
且m≠0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com