
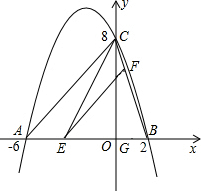
 已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.分析 (1)根据解方程,可得B、C点的坐标,根据函数值相等的点关于对称轴对称,可得A点坐标,根据待定系数法,可得函数解析式;
(2)根据相似三角形的判定与性质,可得EF的长,根据等角的三角函数值相等,可得FG的值,根据三角形面积的和差,可得函数解析式;
(3)分类讨论:N点在x轴上方,N点在x轴下方,根据平行四边形的性质,可得关于a的方程,根据解方程,可得M点的坐标.
解答 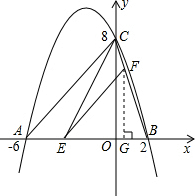 解:(1)x2-10x+16=0,
解:(1)x2-10x+16=0,
解得x1=2,x2=8.
∵点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC),
∴点B的坐标为(2,0),点C的坐标为(0,8).
又由抛物线的对称轴是直线x=-2,得A点坐标为(-6,0),
把A,B,C点坐标代入表达式y=ax2+bx+c,得$\left\{\begin{array}{l}{36a-6b+c=0}\\{4a+2b+c=0}\\{c=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=-\frac{8}{3}}\\{c=8}\end{array}\right.$.
∴所求抛物线的表达式为y=-$\frac{2}{3}$x2-$\frac{8}{3}$x+8.
(2)依题意,AE=m,则BE=8-m,
∵OA=6,OC=8,
∴AC=10.
∵EF∥AC,
∴△BEF∽△BAC,$\frac{EF}{AC}$=$\frac{BE}{AB}$,即$\frac{EF}{10}$=$\frac{8-m}{8}$,
∴EF=$\frac{40-5m}{4}$.
过点F作FG⊥AB,垂足为G,
则sin∠FEG=sin∠CAB=$\frac{4}{5}$,
∴$\frac{FG}{EF}$=$\frac{4}{5}$,FG=$\frac{4}{5}$•$\frac{40-5m}{4}$=8-m,
∴S=S△BCE-S△BFE=$\frac{1}{2}$(8-m)×8-$\frac{1}{2}$(8-m)(8-m)=-$\frac{1}{2}$m2+4m (0<m<8).
(3)存在,理由如下:
设M(a,0),N(x,-$\frac{2}{3}$x2-$\frac{8}{3}$x+8),当点N在x轴上方当时,
$\left\{\begin{array}{l}{AM=NC}\\{MN=AC}\end{array}\right.$即$\left\{\begin{array}{l}{(a+6)^{2}={x}^{2}+(-\frac{2}{3}{x}^{2}-\frac{8}{3}x)^{2}}\\{(x-a)^{2}+(-\frac{2}{3}{x}^{2}-\frac{8}{3}x+8)^{2}=1{0}^{2}}\end{array}\right.$,
解得a1=-10,a2=-2,即M1(-10,0),M2(-2,0);
当点N在x轴上方当时,
$\left\{\begin{array}{l}{AN=MC}\\{MN=AC}\end{array}\right.$,即$\left\{\begin{array}{l}{(x+6)^{2}+(-\frac{2}{3}{x}^{2}-\frac{8}{3}x+8)^{2}={a}^{2}+{8}^{2}}\\{(x-a)^{2}+(-\frac{2}{3}{x}^{2}-\frac{8}{3}x+8)^{2}=1{0}^{2}}\end{array}\right.$,
解得a3=4-2$\sqrt{7}$,a4=4+2$\sqrt{7}$,即M3(4-2$\sqrt{7}$,0),M4(4+2$\sqrt{7}$,0),
综上所述:点M的坐标分别是(-10,0),(-2,0),(4-2$\sqrt{7}$,0),(4+2$\sqrt{7}$,0).
点评 本题考察了二次函数综合题,(1)利用了解方程,待定系数法求函数解析式;(2)利用了相似三角形的判定与性质,等角的三角的三角函数值相等,三角形面积的和差;(3)利用了平行四边形的性质,分类讨论是解题关键,以防遗漏.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
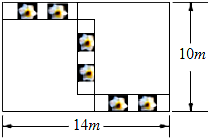 某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为( )
某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为( )| A. | 8 | B. | 13 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 16 | C. | 22 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com