
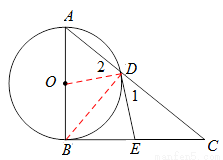
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.

(1)证明见解析;(2)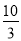 .
.
【解析】
试题分析:(1)连接OD,BD,求出∠ADB=∠BDC=90°,推出DE=BE=CE,推出∠EDB=∠EBD,∠OBD=∠ODB,推出∠EDO=∠EBO=90°即可.
(2)由∠BDC=90°,E为BC边的中点可得BC=4,在Rt△ABC中,由tanC=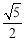 可得AB=2
可得AB=2 ,在Rt△ABC中,由勾股定理可得AC=6,由△ABD∽△ACB可求得AD=
,在Rt△ABC中,由勾股定理可得AC=6,由△ABD∽△ACB可求得AD=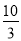 .
.
试题解析:(1)如图,连接BD、OD,
∵AB为⊙O的直径,∴∠ADB=∠BDC=90°.
∵E为BC边的中点,∴DE=EC.∴∠1=∠C.
∵OA=OD,∴∠2=∠A.
∵∠ABC=90°,∴∠A+∠C =90°.∴∠1+∠2 =90°.
∴∠ODE =90°.∴OD⊥DE于点D.
∵以AB为直径的⊙O交AC于点D,∴D是半径的外端.
∴DE与⊙O 相切.
(2)∵∠BDC=90°,E为BC边的中点,∴ 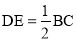 .
.
∵DE=2,∴BC=4.
在Rt△ABC中,tanC=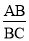 ,∴AB=BC·
,∴AB=BC·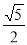 =2
=2 .
.
在Rt△ABC中,AC=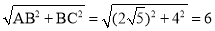 ,
,
又∵△ABD∽△ACB,∴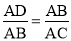 ,即
,即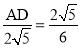 .
.
∴AD=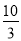 .
.
考点:1.切线的判定;2.圆周角定理;3.等腰三角形的性质;4.三角形内角和定理;5.直角三角形斜边上的中线性质;6.锐角三角函数定义;7.勾股定理;8.相似三角形的判定和性质.


科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
我们规定:形如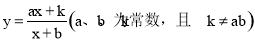 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当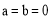 时,“奇特函数”
时,“奇特函数” 就是反比例函数
就是反比例函数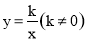 .
.
(1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”;
(2) 如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3).点D是OA的中点,连结OB,CD交于点E,“奇特函数”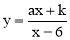 的图象经过B,E两点.
的图象经过B,E两点.
① 求这个“奇特函数”的解析式;
② 把反比例函数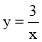 的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为
的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为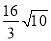 ,请直接写出点P的坐标.
,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:选择题
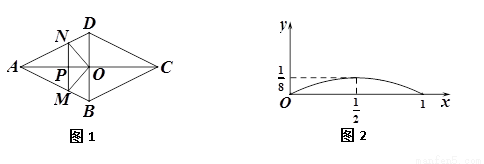
如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为( )
A. 2 B.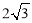 C.4 D.
C.4 D.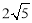
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
端午节期间,某校“慈善小组”筹集善款600元,全部用于购买粽子到福利院送给老人.购买大枣粽子和豆沙粽子各花300元,已知大枣粽子比豆沙粽子每盒贵5元,结果购买的大枣粽子比豆沙粽子少2盒.请求出两种口味的粽子每盒各多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com