练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】随着人们环保意识的不断增强,延安市家庭电动自行车的拥有量逐年增加.据统计,某小区2016年底拥有家庭电动自行车125辆,2018年底家庭电动自行车的拥有量达到180辆.若该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率相同且均为x，则可列方程为( )

    A.125=180B.=180

    C.125(1+x)(1+2x)=180D.125=180

    【答案】D

    【解析】

    设该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率为x，根据该小区2016年底及2018年底家庭电动自行车的拥有量，即可得出关于x的一元二次方程.

    解：设该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率为x，依题意，得：125（1+x）2=180，

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛．该校七、八年级各有学生400人，各随机抽取20名学生进行了抽样调查，获得了他们知识竞赛成绩（单位：分），并对数据进行整理、描述和分析．下面给出了部分信息．

    a．七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率（80分及以上）如下表所示：

    年级

    平均数

    中位数

    众数

    优秀率

    七年级

    84. 2

    77

    74

    45﹪

    b．八年级学生知识竞赛成绩的扇形统计图如下（数据分为5组，A：50≤x≤59； B：60≤x≤69；C：70≤x≤79；D：80≤x≤89；E：90≤x≤100）

    c．八年级学生知识竞赛成绩在D组的是：87 88 88 88 89 89 89 89

    根据以上信息，回答下列问题：

    （1）八年级学生知识竞赛成绩的中位数是 分；

    （2）请你估计该校七、八年级所有学生中达到“优秀”的有多少人？

    （3）下列结论：①八年级成绩的众数是89分；②八年级成绩的平均数可能为86分；③八年级成绩的极差可能为50分．其中所有正确结论的序号是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

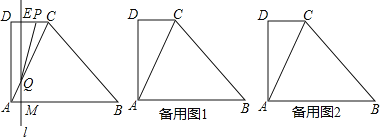
    如图，直角梯形ABCD中，AB∥DC，，，．动点M以每秒1个单位长的速度，从点A沿线段AB向点B运动；同时点P以相同的速度，从点C沿折线C-D-A向点A运动．当点M到达点B时，两点同时停止运动．过点M作直线l∥AD，与线段CD的交点为E，与折线A-C-B的交点为Q．点M运动的时间为t（秒）．

    （1）当时，求线段的长；

    （2）当0＜t＜2时，如果以C、P、Q为顶点的三角形为直角三角形，求t的值；

    （3）当t＞2时，连接PQ交线段AC于点R．请探究是否为定值，若是，试求这个定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将三角形ABC绕点C顺时针旋转90°得到三角形EDC．若点A，D，E在同一条直线上，∠ACB＝20°，求∠ADC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

    （1）求甲、乙两种树苗每棵的价格各是多少元？

    （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（定义学习）

    定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”.

    （判断尝试）

    在A.矩形；B.菱形；C.正方形中；一定是“对直四边形”的是______.(填字母序号)

    （操作探究）

    在菱形ABCD中，AB=2，∠B=60°，AE⊥BC于点E,请用尺规作图法在边AD和CD上各找一点F，使得由点A、E、C、F组成的四边形为“对直四边形”，连接EF，并直接写出EF的长.(保留作图痕迹，不写作法)

    (1)当点F在边AD上时.

    (2)当点F在边CD上时.

    （实践应用）

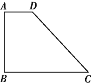
    某加工厂有一批四边形板材，形状如图所示，已知AB=3米，AD=1米，∠C=45°，∠A=∠B=90°.现根据客户要求，需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形”板材，且这两个等腰三角形的腰长相等,要求充分利用材料且无剩余，求分割后得到的等腰三角形的腰长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

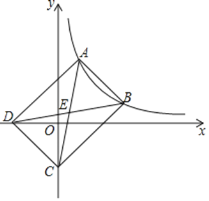
    【题目】如图，点A和点B都是反比例函数在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1，连接AB，以线段AB为边的矩形ABCD的顶点D，C恰好分别落在x轴，y轴的负半轴上，连接AC，BD交于点E，若的面积为6，则k的值为（ ）

    A.2B.3C.6D.12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）我们知道：同弧或等弧所对的圆周角都相等，且等于这条弧所对的圆心角的一半．那么，在一个圆内同一条弦所对的圆周角与圆心角之间又有什么关系？

    （初步思考）（1）如图，是的弦，，点、分别是优弧和劣弧上的点，则______°．_______°．

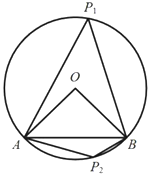
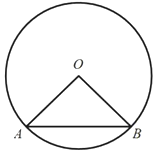
    （2）如图，是的弦，圆心角，点P是上不与A、B重合的一点，求弦所对的圆周角的度数（用m的代数式表示）．

    （问题解决）（3）如图，已知线段，点C在所在直线的上方，且．用尺规作图的方法作出满足条件的点C所组成的图形（不写作法，保留作图痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点O为坐标原点，已知△OAB是等腰直角三角形，且∠OAB＝90°，若点A的坐标（3，1），则点B的坐标为______．

    查看答案和解析>>

    同步练习册答案