
����Ŀ�����������������֪����ͬ����Ȼ����Ե�Բ�ܽǶ���ȣ��ҵ������������Ե�Բ�Ľǵ�һ�룮��ô����һ��Բ��ͬһ�������Ե�Բ�ܽ���Բ�Ľ�֮������ʲô��ϵ��
������˼������1����ͼ��![]() ��
��![]() ���ң�
���ң�![]() ����
����![]() ��
��![]() �ֱ����Ż�
�ֱ����Ż�![]() ���ӻ�
���ӻ�![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ______����
______����![]() _______����
_______����
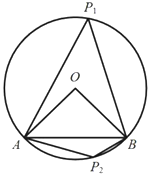
��2����ͼ��![]() ��
��![]() ���ң�Բ�Ľ�
���ң�Բ�Ľ�![]() ����P��
����P��![]() �ϲ���A��B�غϵ�һ�㣬����
�ϲ���A��B�غϵ�һ�㣬����![]() ���Ե�Բ�ܽ�
���Ե�Բ�ܽ�![]() �Ķ�������m�Ĵ���ʽ��ʾ����
�Ķ�������m�Ĵ���ʽ��ʾ����
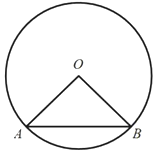
������������3����ͼ����֪�߶�![]() ����C��
����C��![]() ����ֱ�ߵ��Ϸ�����
����ֱ�ߵ��Ϸ�����![]() ���ó߹���ͼ�ķ����������������ĵ�C����ɵ�ͼ�Σ���д������������ͼ�ۼ�����
���ó߹���ͼ�ķ����������������ĵ�C����ɵ�ͼ�Σ���д������������ͼ�ۼ�����
![]()
���𰸡���1����1��50����130������2��![]() ����3��������
����3��������
��������
��1������ͬ����Ȼ����Ե�Բ�ܽǶ���ȣ��ҵ������������Ե�Բ�Ľǵ�һ�룬���ɵý⣻
��2�����Ƚ���P��������ۣ��Ż����ӻ���Ȼ��ֱ�Ӹ���ͬ����Ȼ����Ե�Բ�ܽǶ���ȣ��ҵ������������Ե�Բ�Ľǵ�һ�룬���ɵý⣻
��3�����ݣ�2�������ý��ۣ���AB���е�ΪԲ�ģ�ABΪֱ����Բ��Ȼ���Բ�������䴹ֱ��ֱ������Բ��D��E���㣬����DΪԲ�ģ�DBΪ�뾶��Բ���ӻ�AB��Ϊ����.
��1���������⣬��
![]() ��
��
![]()
��2����P���Ż�![]() ��ʱ
��ʱ![]()
��![]() ���ӻ�
���ӻ�![]() ��ʱ��
��ʱ��![]() ��
��
��![]()
��3����ͼ��ʾ��
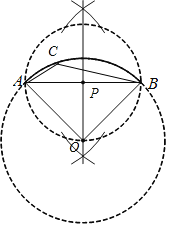
��ͼ��Ϊ�����ӻ�![]() ����
����


 ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д� ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����ҵ�Ŷ�ץס�̻�������һ���ɹ���װ��Ӫ�����������С��װ����ۣ�ÿ���ɱ�3Ԫ�������ڼ䷢��ÿ���������y�����������۵���x��Ԫ��֮������һ�κ�����ϵ���������������ʾ������3.5��x��5.5������ÿ�컹��֧�������������80Ԫ��
���۵���x��Ԫ�� | 3.5 | 5.5 |
������y������ | 280 | 120 |
��1����ֱ��д��y��x֮��ĺ�����ϵʽ��
��2�����ÿ����160Ԫ���������۵���Ϊ����Ԫ��
��3����ÿ�������ΪwԪ�������۵��۶�Ϊ����Ԫʱ��ÿ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ǻ�����ʶ�IJ�����ǿ,�Ӱ��м�ͥ�綯���г���ӵ������������.��ͳ��,ijС��2016���ӵ�м�ͥ�綯���г�125��,2018���ͥ�綯���г���ӵ�����ﵽ180��.����С��2016���2018���ͥ�綯���г�ӵ������ƽ����������ͬ�Ҿ�Ϊx������з���Ϊ( )
A.125![]() =180B.
=180B.![]() =180
=180
C.125(1+x)(1+2x)=180D.125![]() =180
=180
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ�����ǽ�ɽ��ɽ����Ϊ�˸�����̬������ij���������Ծ��ں����������١���ͨ�ӵ���ͬʱ����Ⱥ�ܼ����غ��������Ӳ�����������̬ʪ�ع�.
��1��2018��11����12�£�һ�ڹ���ԭ�ƻ���ͨ�ӵ��������Ӳ������������20ǧ�ף����������Ӳ������������ͨ�ӵ��������![]() ������ô��ԭ�ƻ������Ӳ�������ǧ�ף�
������ô��ԭ�ƻ������Ӳ�������ǧ�ף�
��2����2018��12�µף�һ�ڹ���˳����ԭ�ƻ�����ܹ�����840��Ԫ��������ͨ�ӵ����̹�����600��Ԫ��2019����ڹ��̿�������ͨ�ӵ�ÿǧ���̷��ý�һ�ڽ���2.5a�����������һ������3a���������Ӳ���ÿǧ���̷��ý�һ������2.5a�����������һ������5a���������㣬���ڹ����ܷ��ý���һ������2a������a��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() .
.
��1��֤���÷���һ������������ȵ�ʵ������
��2����÷�������Ϊx1��x2��x1<x2��.
�ٵ�![]() ʱ����ȷ��yֵ�ķ�Χ��
ʱ����ȷ��yֵ�ķ�Χ��
����ͼ��ƽ��ֱ������ϵ��������A��B��C������ֱ�Ϊ��x1,0������x2,3������7��0��.�Ե�CΪԲ�ģ�2����λ����Ϊ�뾶��Բ��ֱ��AB���У���n��ֵ.
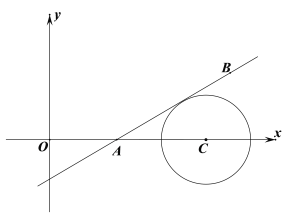
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ���й�������Ϊ30Ԫ��ͯװ���ɼ�����۲��Ź涨�����۵��۲�����ÿ��30Ԫ��������ÿ��60Ԫ������һ��ʱ����֣������۵���Ϊ60Ԫʱ��ƽ��ÿ��������Ϊ80�����������۵���ÿ����10Ԫʱ��ƽ��ÿ���ܶ��۳�20����ͬʱ�������۹����У�ÿ�»�Ҫ֧����������450Ԫ�������۵���ΪxԪ��ƽ����������Ϊy����
��1�����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�������۵���Ϊ����Ԫʱ����������ͯװÿ�¿ɻ���1800Ԫ��
��3�������۵���Ϊ����Ԫʱ����������ͯװÿ�»�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��У�յ�����һ��ǽ������Ϊ20m���ó�Ϊ32m����ʺ�����ǽΧ��һ�����λ��ԣ���ͼ��ʾ��
��1����Χ�������126m2�ľ��λ��������ܣ������˵���������ܣ���˵�����ɣ�
��2�������������4m��Χ�ɵľ��λ�������ܴﵽ170m2����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��x2+2x+m��
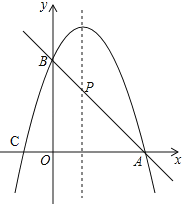
��1����������߹���A��3��0������y�ύ�ڵ�B���������ߵĽ���ʽ����B��C�����ꣻ
��2����ͼ��ֱ��AB�����������ߵĶԳ��ύ�ڵ�P����ֱ��AB�ı���ʽ�͵�P�����꣮
��3������������һ��D��x��y����ʹ��S��ABC=S��ACD�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����y��mx��m�ͺ���y��mx2��2x��2 (m�dz�������m��0)��ͼ������ǣ� ��
A.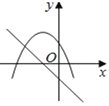 B.
B.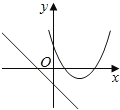 C.
C.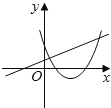 D.
D.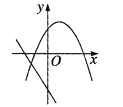
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com