
ЁОЬтФПЁПЃЈЖЈвхбЇЯАЃЉ
ЖЈвх:ШчЙћЫФБпаЮгавЛзщЖдНЧЮЊжБНЧ,ФЧУДЮвУЧГЦетбљЕФЫФБпаЮЮЊЁАЖджБЫФБпаЮЁБ.
ЃЈХаЖЯГЂЪдЃЉ
дкA.ОиаЮЃЛB.СтаЮЃЛC.е§ЗНаЮжаЃЛвЛЖЈЪЧЁАЖджБЫФБпаЮЁБЕФЪЧ______.(ЬюзжФИађКХ)
ЃЈВйзїЬНОПЃЉ
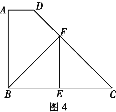
дкСтаЮABCDжаЃЌAB=2ЃЌЁЯB=60ЁуЃЌAEЁЭBCгкЕуE,ЧыгУГпЙцзїЭМЗЈдкБпADКЭCDЩЯИїеввЛЕуFЃЌЪЙЕУгЩЕуAЁЂEЁЂCЁЂFзщГЩЕФЫФБпаЮЮЊЁАЖджБЫФБпаЮЁБЃЌСЌНгEFЃЌВЂжБНгаДГіEFЕФГЄ.(БЃСєзїЭМКлМЃЃЌВЛаДзїЗЈ)
(1)ЕБЕуFдкБпADЩЯЪБ.
(2)ЕБЕуFдкБпCDЩЯЪБ.

ЃЈЪЕМљгІгУЃЉ
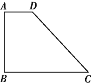
ФГМгЙЄГЇгавЛХњЫФБпаЮАхВФЃЌаЮзДШчЭМЫљЪОЃЌвбжЊAB=3УзЃЌAD=1УзЃЌЁЯC=45ЁуЃЌЁЯA=ЁЯB=90Ёу.ЯжИљОнПЭЛЇвЊЧѓЃЌашНЋУПеХЫФБпаЮАхВФНјвЛВНЗжИюГЩСНИіЕШбќШ§НЧаЮАхВФКЭвЛИіЁАЖджБЫФБпаЮЁБАхВФЃЌЧветСНИіЕШбќШ§НЧаЮЕФбќГЄЯрЕШ,вЊЧѓГфЗжРћгУВФСЯЧвЮоЪЃгрЃЌЧѓЗжИюКѓЕУЕНЕФЕШбќШ§НЧаЮЕФбќГЄ.
ЁОД№АИЁПЁОХаЖЯГЂЪдЁПAЃЌCЃЛЁОВйзїЬНОПЁП(1)ЭММћНтЮіЃЌEF=2ЃЛ(2)ЭММћНтЮіЃЌEF=![]() ЃЛЁОЪЕМљгІгУЁПЕШбќШ§НЧаЮЕФбќГЄЮЊ
ЃЛЁОЪЕМљгІгУЁПЕШбќШ§НЧаЮЕФбќГЄЮЊ![]() УзЛђ2Уз.
УзЛђ2Уз.
ЁОНтЮіЁП
ХаЖЯГЂЪдЃКжБНгИљОнЁАЖджБЫФБпаЮЁБЖЈвхПЩЕУЃКОиаЮКЭе§ЗНаЮЪЧЁАЖджБЫФБпаЮЁБЃЛ
ВйзїЬНОПЃК
ЃЈ1ЃЉFдкБпADЩЯЪБЃЌШчЭМ1ЃЌзїCFЁЭADЃЌЕУОиаЮAECFЃЌИљОнЙДЙЩЖЈРэПЩЕУEFЕФГЄЃЛ
ЃЈ2ЃЉFдкБпCDЩЯЪБЃЌШчЭМ2ЃЌзїAFЁЭCDЃЌжЄУїЁїAEFЪЧЕШБпШ§НЧаЮЃЌПЩЕУEFЕФГЄЃЛ
ЪЕМљгІгУЃК
ДцдкСНжжЧщПіЃКЂйШчЭМ3ЃЌОиаЮABEDЃЌFЪЧDCЕФжаЕуЃЌЂкШчЭМ4ЃЌЁЯA=ЁЯBFD=90ЁуЃЌEЪЧBCЕФжаЕуЃЌИљОнжБНЧШ§НЧаЮаББпжаЯпЕШгкаББпвЛАыПЩЕУНсТлЃЎ
Нт:ЁОХаЖЯГЂЪдЁПЁпОиаЮЕФЫФИіФкНЧЖМЪЧжБНЧЃЌе§ЗНаЮЕФЫФИіФкНЧЖМЪЧжБНЧЃЌ
ЁрОиаЮКЭе§ЗНаЮЕФЖдНЧЮЊжБНЧ,ЮЊЁАЖджБЫФБпаЮЁБ
ЙЪЬюЃКAЃЌC.
ВйзїЬНОПЃК
(1)ЕБЕуFдкБпADЩЯЪБ,ШчЭМ1,
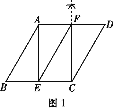
гЩЬтвтПЩЕУЁЯAEC=ЁЯAFC=90Ёу,
дкRtЁїABEжа,ЁЯB=60Ёу,
ЁрЁЯBAE=30Ёу.
ЁпAB=BC=2,
ЁрBE=1,
ЁрCE=2-1=1.
ЁпADЁЮBC,AEЁЭBC,CFЁЭAD,
ЁрAE=CF=![]() =
=![]() ,
,
ЁрEF=![]() =2.
=2.
(2)ЕБЕуFдкБпCDЩЯЪБ,ШчЭМ2,
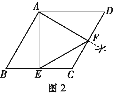
гЩЬтвтПЩЕУAFЁЭCD.
ЁпЫФБпаЮABCDЪЧСтаЮ,
ЁрAB=AD,ЁЯB=ЁЯD=60Ёу.
ЁпЁЯAEB=ЁЯAFD=90Ёу,
ЁрЁїABEЁеЁїADF(AAS),
ЁрAE=AF.
ЁпЁЯBAE=ЁЯDAF=30Ёу,
ЁрЁЯEAF=120Ёу-30Ёу-30Ёу=60Ёу,
ЁрЁїAEFЪЧЕШБпШ§НЧаЮ,
ЁрEF=AE=![]() .
.
ЪЕМљгІгУЃК
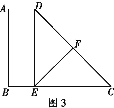
ЂйШчЭМ3ЃЌдкОиаЮABEDжаЃЌFЪЧDCЕФжаЕу,
дкRtЁїDECжаЃЌЁЯC=45Ёу,
ЁрЁїDECЪЧЕШбќжБНЧШ§НЧаЮ,
ЧвDE=EC=3ЃЌ
ЁрDC=3![]() ЃЌ
ЃЌ
ЁрDF=CF=EF=![]() ЃЌМДДЫЪБЗжИюКѓЕУЕНЕФЕШбќШ§НЧаЮЕФбќГЄЮЊ
ЃЌМДДЫЪБЗжИюКѓЕУЕНЕФЕШбќШ§НЧаЮЕФбќГЄЮЊ![]() УзЃЛ
УзЃЛ
ЂкШчЭМ4ЃЌЁЯA=ЁЯBFD=90ЁуЃЌEЪЧBCЕФжаЕу,
ЭЌРэЕУЁїBFCЪЧЕШбќжБНЧШ§НЧаЮ.
ЁпBC=4ЃЌ
ЁрEF=BE=CE=2ЃЌМДДЫЪБЗжИюКѓЕУЕНЕФЕШбќШ§НЧаЮЕФбќГЄЮЊ2Уз.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§y=ax2+bx+cЭМЯѓЕФвЛ.ВПЗжЃЌЧвЙ§Еу(-3ЃЌ0)ЃЌ(1ЃЌ0)ЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
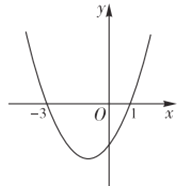
A.2a-b=0
B.4a-2bЪЎc<0.
C.Шє(-4ЃЌy1)ЃЌ( ![]() ЃЌy2)ЪЧХзЮяЯпЩЯСНЕуЃЌдђy1> y2
ЃЌy2)ЪЧХзЮяЯпЩЯСНЕуЃЌдђy1> y2
D.y <0ЪБЃЌ-3<x < 1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНЉx2+bx+cЃЌКЏЪ§жЕyгыздБфСПxжЎМфЕФВПЗжЖдгІжЕШчЯТБэЃК
x | Ё | Љ4 | Љ1 | 0 | 1 | Ё |
y | Ё | Љ2 | Љ1 | Љ2 | Љ7 | Ё |
ЃЈ1ЃЉДЫЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсЪЧжБЯпЃЌДЫКЏЪ§ЭМЯѓгыxжсНЛЕуИіЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧѓЖўДЮКЏЪ§ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉЕБЉ5ЃМxЃМЉ1ЪБЃЌЧыжБНгаДГіКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019ФъХЎХХЪРНчБжаЃЌжаЙњХЎХХвд11еОШЋЪЄЧвжЛЖЊ3ОжЕФГЩМЈГЩЙІЮРУсБОНьЪРНчБЙкОќ.ФГаЃЦпФъМЖЮЊСЫКыбяХЎХХОЋЩёЃЌзщНЈСЫХХЧђЩчЭХЃЌЭЈЙ§ВтСПЭЌбЇУЧЕФЩэИп(ЕЅЮЛЃКcm)ЃЌВЂЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыНсКЯЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬт.

(1)ЬюПеЃКбљБОШнСПЮЊ___ЃЌa=___ЃЛ
(2)АбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
(3)ШєДгИУзщЫцЛњГщШЁ1УћбЇЩњЃЌЙРМЦетУћбЇЩњЩэИпЕЭгк165cmЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХШЫУЧЛЗБЃвтЪЖЕФВЛЖЯдіЧП,бгАВЪаМвЭЅЕчЖЏздааГЕЕФгЕгаСПж№ФъдіМг.ОнЭГМЦ,ФГаЁЧј2016ФъЕзгЕгаМвЭЅЕчЖЏздааГЕ125СО,2018ФъЕзМвЭЅЕчЖЏздааГЕЕФгЕгаСПДяЕН180СО.ШєИУаЁЧј2016ФъЕзЕН2018ФъЕзМвЭЅЕчЖЏздааГЕгЕгаСПЕФЦНОљдіГЄТЪЯрЭЌЧвОљЮЊxЃЌдђПЩСаЗНГЬЮЊ( )
A.125![]() =180B.
=180B.![]() =180
=180
C.125(1+x)(1+2x)=180D.125![]() =180
=180
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
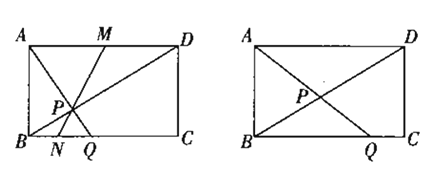
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=a,AD=b,ЕуPЪЧЖдНЧЯпBDЩЯЕФвЛИіЖЏЕуЃЈЕуPВЛгыBЁЂDжиКЯЃЉЃЌСЌНгAPВЂбгГЄНЛЩфЯпBCгкЕуQЃЌ
ЃЈ1ЃЉЕБAPЁЭBDЪБЃЌЧѓЁїABQЕФУцЛ§ЃЈгУКЌaЁЂbЕФДњЪ§ЪНБэЪОЃЉ.
ЃЈ2ЃЉШєЕуMЮЊADБпЕФжаЕуЃЌСЌНгMPНЛBCгкЕуNЃЌжЄУїЃКЕуNвВЮЊЯпЖЮBQЕФжаЕу.
ЃЈ3ЃЉШчЭМЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЁїADPгыЁїBPQЕФУцЛ§жЎКЭзюаЁ.
ЮЊКЮжЕЪБЃЌЁїADPгыЁїBPQЕФУцЛ§жЎКЭзюаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАТЬЫЎЧрЩНЃЌОЭЪЧН№ЩНвјЩНЁБЃЌЮЊСЫИФЩЦЩњЬЌЛЗОГЃЌФГЯиеўИЎзМБИЖдОГФкКгСїНјааЧхгйЁЂЪшЭЈКгЕРЃЌЭЌЪБдкШЫШКУмМЏЧјбиКгСїаоНЈБѕКгВНЕРЃЌДђдьЩњЬЌЪЊЕиЙЋдА.
ЃЈ1ЃЉ2018Фъ11дТжС12дТЃЌвЛЦкЙЄГЬдМЦЛЎЪшЭЈКгЕРКЭаоНЈБѕКгВНЕРРяГЬЪ§ЙВМЦ20ЧЇУзЃЌЦфжааоНЈБѕКгВНЕРРяГЬЪ§ЪЧЪшЭЈКгЕРРяГЬЪ§ЕФ![]() БЖЃЌФЧУДЃЌдМЦЛЎаоНЈБѕКгВНЕРЖрЩйЧЇУзЃП
БЖЃЌФЧУДЃЌдМЦЛЎаоНЈБѕКгВНЕРЖрЩйЧЇУзЃП
ЃЈ2ЃЉжС2018Фъ12дТЕзЃЌвЛЦкЙЄГЬЫГРћАДдМЦЛЎЭъГЩзмЙВКФзЪ840ЭђдЊЃЌЦфжаЪшЭЈКгЕРЙЄГЬЙВКФзЪ600ЭђдЊЃЛ2019ФъЖўЦкЙЄГЬПЊЙЄКѓЃЌЪшЭЈКгЕРУПЧЇУзЙЄГЬЗбгУНЯвЛЦкНЕЕЭ2.5aЃЅЃЌРяГЬЪ§НЯвЛЦкдіМг3aЃЅЃЛаоНЈБѕКгВНЕРУПЧЇУзЙЄГЬЗбгУНЯвЛЦкЩЯеЧ2.5aЃЅЃЌРяГЬЪ§НЯвЛЦкдіМг5aЃЅЃЌОВтЫуЃЌЖўЦкЙЄГЬзмЗбгУНЋБШвЛЦкдіМг2aЃЅЃЌЧѓaЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЗўзАГЌЪаЙКНјЕЅМлЮЊ30дЊЕФЭЏзАШєИЩМўЃЌЮяМлВПУХЙцЖЈЦфЯњЪлЕЅМлВЛЕЭгкУПМў30дЊЃЌВЛИпгкУПМў60дЊЃЎЯњЪлвЛЖЮЪБМфКѓЗЂЯжЃКЕБЯњЪлЕЅМлЮЊ60дЊЪБЃЌЦНОљУПдТЯњЪлСПЮЊ80МўЃЌЖјЕБЯњЪлЕЅМлУПНЕЕЭ10дЊЪБЃЌЦНОљУПдТФмЖрЪлГі20МўЃЎЭЌЪБЃЌдкЯњЪлЙ§ГЬжаЃЌУПдТЛЙвЊжЇИЖЦфЫћЗбгУ450дЊЃЎЩшЯњЪлЕЅМлЮЊxдЊЃЌЦНОљдТЯњЪлСПЮЊyМўЃЎ
ЃЈ1ЃЉЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЯњЪлетжжЭЏзАУПдТПЩЛёРћ1800дЊЃП
ЃЈ3ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЯњЪлетжжЭЏзАУПдТЛёЕУРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌBCЕФДЙжБЦНЗжЯпEFНЛЁЯABCЕФЦНЗжЯпBDгкEЃЌШчЙћЁЯBAC=60ЁуЃЌЁЯACE=24ЁуЃЌФЧУДЁЯBCEЕФДѓаЁЪЧЃЈЁЁЁЁЃЉ

A. 24Ёу B. 30Ёу C. 32Ёу D. 36Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com