
分析 先把方程化为一般式,再计算判别式的值得到△=4m2-8m+32,接着利用配方法得到△=4(m-1)2+28,根据非负数的性质可判断△>0,然后根据根与系数的关系,当AB+AC=2m>0,AB•AC=2m-8>0,AB与AC都为正数,解得m>4,于是得到当m>4时,这样的三角形存在.
解答 解:x2-2mx+2m-8=0,
△=4m2-4(2m-8)
=4m2-8m+32
=4(m-1)2+28,
∵(m-1)2≥0,
∴△>0,
∵AB+AC=2m,AB•AC=2m-8,
∴当2m>0且2m-8>0时,AB与AC的值存在,此时m>4,
∴当m>4时,这样的三角形存在.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
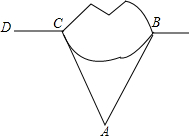 一个工程队在修路时要开挖一条笔直的隧道,如图所示,经测定,点B、C、D在同一条直线上,为加快施工进度,要在B、C两端同时施工,现在山外一点A(可直达B、C两点)测得∠A=55°,∠ACD=105°.问:在B点的施工队应按与BA成多少度角的方向施工,隧道才能在山中顺利接通?为什么?
一个工程队在修路时要开挖一条笔直的隧道,如图所示,经测定,点B、C、D在同一条直线上,为加快施工进度,要在B、C两端同时施工,现在山外一点A(可直达B、C两点)测得∠A=55°,∠ACD=105°.问:在B点的施工队应按与BA成多少度角的方向施工,隧道才能在山中顺利接通?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com