练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解方程：

    (1)5x﹣1＝x+1

    (2)2x+3(2x﹣1)＝16﹣(x+1)

    (3)

    (4)

    【答案】⑴

    ⑵ 2

    ⑶

    ⑷

    【解析】

    ⑴首先将未知数移动到等号左边，将常数项移到等式右边，然后进行相应计算即可求出未知量.

    ⑵去括号，将未知数移动到等号左边，将常数项移到等式右边，然后进行相应计算即可求出未知量.

    ⑶先通分，将未知数移动到等号左边，将常数项移到等式右边，然后进行相应计算即可求出未知量.

    ⑷先通分，将未知数移动到等号左边，将常数项移到等式右边，然后进行相应计算即可求出未知量.

    解：⑴5x-1=x+1

    4x=2

    x=

    ⑵2x+3(2x-1)=16-(x+1)

    2x+6x-3=16-x-1

    9x=18

    x=

    ⑶

    3(3x-1)-4(x+2)=12

    9x-3-4x-8=12

    5x=23

    x=

    ⑷ 原方程变形为：50(0.1x-0.2)-2(x+1)=1

    5x-10-2x-2=1

    3x=13

    x=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于（ ）

    A. 4：2：1 B. 5：3：1 C. 25：12：5 D. 51：24：10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

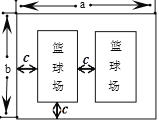
    【题目】今年假期某校对操场进行了维修改造，如图是操场的一角.在长为米，宽为米的长方形场地中间，并排着两个大小相同的篮球场，这两个篮球场之间以及篮球场与长方形场地边沿的距离都为米.

    (1)直接写出一个篮球场的长和宽；(用含字母，，的代数式表示)

    (2)用含字母，，的代数式表示这两个篮球场占地面积的和，并求出当，，时，这两个篮球场占地面积的和.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的周长为16，若∠BAD=60°，E是AB的中点，则点E的坐标为（ ）

    A. (1，1)B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】人和人之间讲友情，有趣的是，数与数之间也有相类似的关系. 若两个不同的自然数的所有真因数（即除了自身以外的正约数）之和相等，我们称这两个数为“亲和数”. 例如：18的约数有1、2、3、6、9、18，它的真因数之和1+2+3+6+9=21；51的约数有1、3、17、51，它的真因数之和1+3+17=21，所以18和51为“亲和数”. 数还可以与动物形象地联系起来，我们称一个两头（首位与末位）都是的数为“两头蛇数”.

    （1）6的“亲和数”为 ；将一个四位的“两头蛇数”去掉两头，得到一个两位数，它恰好是这个“两头蛇数”的约数,求满足条件的“两头蛇数”.

    （2）已知两个“亲和数”的真因数之和都等于15，且这两个“亲和数”中较大的数能将一个正中间数位（百位）上的数为4的五位“两头蛇数”整除，若这个五位“两头蛇数”的千位上的数字小于十位上的数字，求满足条件的“两头蛇数”.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司为了了解员工每人所创年利润情况，公司从各部抽取部分员工对每年所创利润进行统计，并绘制如图1，图2统计图．

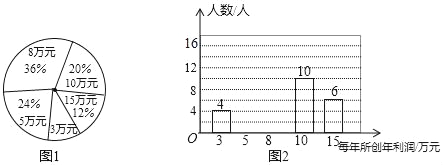
    （1）将图2补充完整；

    （2）本次共抽取员工　 　人，每人所创年利润的众数是　 　万元，平均数是　 　万元，中位数是　 　万元；

    （3）若每人创造年利润10万元及（含10万元）以上为优秀员工，在公司1200员工中有多少可以评为优秀员工？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列两个等式：2=2×+1，5=5×+1，给出定义如下：我们称使等式ab＝ab＋1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对（2，），（5，），都是“共生有理数对”．

    (1)判断数对(2,1),(3,)是不是“共生有理数对”，写出过程；

    (2)若(a,3)是“共生有理数对”，求a的值；

    (3)若(m,n)是“共生有理数对”,则(n,m)“共生有理数对”(填“是”或“不是”)；说明理由；

    (4)请再写出一对符合条件的“共生有理数对”为(注意：不能与题目中已有的“共生有理数对”重复).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】你知道为什么任何无限循环小数都可以写成分数形式吗？下面的解答会告诉你方法.

    （1）阅读下列材料：

    问题：利用一元一次方程将化成分数.

    解：设.

    方程两边都乘以10，可得.

    由和，可得

    即.（请你体会将方程两边都乘以10起到的作用）

    解得，即.

    填空：将写成分数形式为 .

    （2）请你仿照上述方法把小数化成分数，要求写出利用一元一次方程进行解答的过程.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

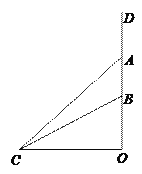
    【题目】如图，水渠边有一棵大木瓜树，树干（不计粗细）上有两个木瓜， （不计大小），树干垂直于地面，量得m，在水渠的对面与处于同一水平面的处测得木瓜的仰角为45°、木瓜的仰角为30°．求处到树干的距离（结果精确到1m）（参考数据： ， ）．

    查看答案和解析>>

    同步练习册答案