
【题目】某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创利润进行统计,并绘制如图1,图2统计图.
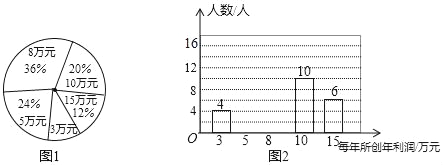
(1)将图2补充完整;
(2)本次共抽取员工 人,每人所创年利润的众数是 万元,平均数是 万元,中位数是 万元;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
【答案】(1)补图见解析;(2)50;8;8.12;8;(3)384
【解析】试题分析:(1)根据扇形统计图计算3万元的员工的百分比为8%,进而结合条形统计图得到抽取员工的总数为50人,得到5万元的员工人数和8万元的员工人数,据此补全统计图;
(2)3万元的员工的百分比为8%,人数为4人,所以抽取员工总数为:4÷8%=50人,每人所创年利润的众数即出现次数最多的数8万元,利用求平均数的公式求平均数;
(3)先计算每人创造年利润10万元及(含10万元)以上的比例,然后计算1200员工中有多少人达到优秀.
试题解析:解:(1)3万元的员工的百分比为:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取员工总数为:4÷8%=50(人),
5万元的员工人数为:50×24%=12(人),
8万元的员工人数为:50×36%=18(人),
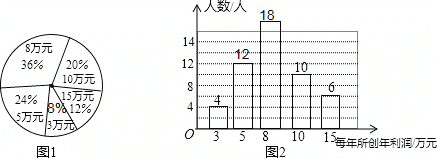
(2)抽取员工总数为:4÷8%=50(人),
每人所创年利润的众数是 8万元,
平均数是:![]() ×(3×4+5×12+8×18+10×10+15×6)=8.12万元.
×(3×4+5×12+8×18+10×10+15×6)=8.12万元.
故答案为:50;8万元;8.12万元.
(3)1200×![]() =384(人),
=384(人),
答:在公司1200员工中有384人可以评为优秀员工.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多肉植物是指植物营养器官肥大的植物,又称肉质植物或多肉花卉,由于体积小、外形萌、色彩斑斓,茶几阳台摆放方便,近年来越来越受到广大养花爱好者的喜爱.多肉植物则被亲切地称为“肉肉”、“多肉君”.大学毕业生陈江河发现这个商机后,第一次果断购进甲乙两种多肉植物共500株.甲种多肉植物每株成本5元,售价10元;乙种多肉植物每株成本8元,售价10元.
(1)由于启动资金有限,第一次购进多肉植物的金额不得超过3400元,则甲种多肉植物至少购进多少株?
(2)多肉植物一经上市,十分抢手,陈江河决定第二次购进甲乙两种多肉植物,它们的进价不变.甲种多肉植物进货量在(1)的最少进货量的基础上增加了![]() ,售价也提高了
,售价也提高了![]() ;乙种多肉植物的售价和进货量不变,但是由于乙种多肉植物的耐热性不强,导致销售完之前它的成活率为
;乙种多肉植物的售价和进货量不变,但是由于乙种多肉植物的耐热性不强,导致销售完之前它的成活率为![]() .结果第二次共获利2700元.求m的值.
.结果第二次共获利2700元.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:

(1)第①行的第n个数是_______(直接写出答案,n为正整数)
(2)第②、③行的数与第①行相对应的数分别有什么关系?
(3)取每行的第9个数,记这三个数的和为a,化简计算求值:(5a2-13a-1)-4(4-3a+![]() a2)
a2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() .
.
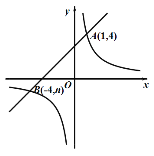
(1)求k和b的值;
(2)连接OA、OB,求![]() 的面积;
的面积;
(3)利用图像,直接写出![]() 时x的取值范围.
时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com