
【题目】已知抛物线G:![]() 有最低点。
有最低点。
(1)求二次函数![]() 的最小值(用含m的式子表示);
的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
【答案】(1)二次函数的最小值是![]() ;(2)
;(2)![]() ;(3)-4
;(3)-4![]() -3.
-3.
【解析】
(1)抛物线有最低点即开口向上,m>0,用配方法或公式法求得对称轴和函数最小值.
(2)写出抛物线G的顶点式,根据平移规律即得到抛物线G1的顶点式,进而得到抛物线G1顶点坐标(m+1,-m-3),即x=m+1,y=-m-3,x+y=-2即消去m,得到y与x的函数关系式.再由m>0,即求得x的取值范围.
(3)求出抛物线恒过点B(2,-4),函数H图象恒过点A(2,-3),由图象可知两图象交点P应在点A、B之间,即点P纵坐标在A、B纵坐标之间.
解:(1)∵y=mx2-2mx-3=m(x-1)2-m-3,抛物线有最低点,
∴二次函数y=mx2-2mx-3的最小值为-m-3.
(2)∵抛物线G:y=m(x-1)2-m-3,
∴平移后的抛物线G1:y=m(x-1-m)2-m-3,
∴抛物线G1顶点坐标为(m+1,-m-3),
∴x=m+1,y=-m-3,
∴x+y=m+1-m-3=-2.
即x+y=-2,变形得y=-x-2.
∵m>0,m=x-1.
∴x-1>0,
∴x>1,
∴y与x的函数关系式为y=-x-2(x>1).
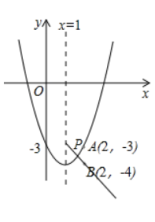
(3)如图,函数H:y=-x-2(x>1)图象为射线,
x=1时,y=-1-2=-3;x=2时,y=-2-2=-4,
∴函数H的图象恒过点B(2,-4),
∵抛物线G:y=m(x-1)2-m-3,
x=1时,y=-m-3;x=2时,y=m-m-3=-3.
∴抛物线G恒过点A(2,-3),
由图象可知,若抛物线与函数H的图象有交点P,则yB<yP<yA,
∴点P纵坐标的取值范围为-4<yP<-3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
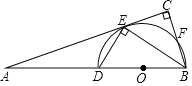
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点F,且E为弧DF的中点.
(1)求证:AC是半圆O的切线;
(2)若BC=8,BE=6![]() ,求半径的长.
,求半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据。
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率mn | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是______;(保留小数点后两位)
(2)估算袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树形图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线的顶点.
是抛物线的顶点.
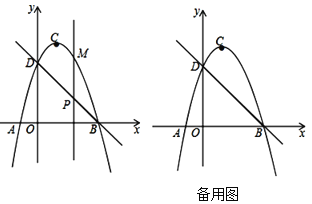
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一个动点,其横坐标为
上方抛物线上的一个动点,其横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,当线段
,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的值及
的值及![]() 的最大值.
的最大值.
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2![]() ,∠BAC=120°,D为BC边上的点,将DA绕D点逆时针旋转120°得到DE.
,∠BAC=120°,D为BC边上的点,将DA绕D点逆时针旋转120°得到DE.
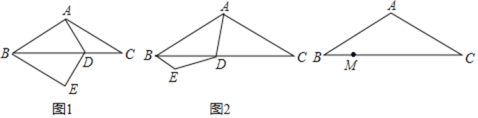
(1)如图1,若AD=DC,则BE的长为 ,BE2+CD2与AD2的数量关系为 ;
(2)如图2,点D为BC边山任意一点,线段BE、CD、AD是否依然满足(1)中的关系,试证明;
(3)M为线段BC上的点,BM=1,经过B、E、D三点的圆最小时,记D点为D1,当D点从D1处运动到M处时,E点经过的路径长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
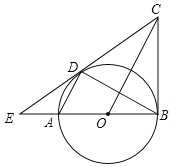
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com