
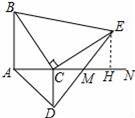
如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为 .


4 .
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】如图作EH⊥AN于H,由△ABC≌△HCE得AB=CH,AC=EH,再证明△ABC≌△HCE得CM=CH即可解决问题.
【解答】解:如图作EH⊥AN于H,
∵BA⊥AN,EH⊥AN,
∴∠BAC=∠EHC=90°,
∵∠ABC+∠ACB=90°,∠ACB+∠ECH=90°,
∴∠ABC=∠ECH,
∵△BCE和△ACD都是等腰三角形,
∴BC=CE,AC=DC,∠BCE=∠ACD=90°
在△ABC和△HCE中,
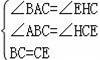

∴△ABC≌△HCE,
∴AC=EH=CD=EH,AB=CH,
在△DCM和△EHM中,
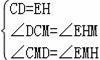
 ,
,
∴△ABC≌△HCE.
∴CM=HM,
∴CM=
 CH=
CH=
 AB=4.
AB=4.
故答案为4.

【点评】本题考查全等三角形的判定和性质、等腰直角三角形的性质,解题的关键是添加辅助线构造全等三角形,掌握添加辅助线的方法,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图所示,在平面直角坐标系中,双曲线y=
 (x<0)上有一点A(﹣2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
(x<0)上有一点A(﹣2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
(1)当点C运动时,四边形ADBE的形状能变成菱形吗?如果能,求出此时点C的位置,若不能,说明理由.
(2)小明经过探究发现:点C运动会影响四边形ADBE形状,但是AD与BE的位置关系始终不变,请你帮他解释其中的原因.


查看答案和解析>>
科目:初中数学 来源: 题型:
下列调查中,最适合用普查方式的是( )
A.调查某品牌牛奶质量合格率
B.调查某幼儿园一班学生的平均身高
C.调查某市中小学生收看纪念抗日战争胜利70周年大阅兵的情况
D.调查某省九年级学生一周内网络自主学习的情况
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com