
如图所示,在平面直角坐标系中,双曲线y=
 (x<0)上有一点A(﹣2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
(x<0)上有一点A(﹣2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
(1)当点C运动时,四边形ADBE的形状能变成菱形吗?如果能,求出此时点C的位置,若不能,说明理由.
(2)小明经过探究发现:点C运动会影响四边形ADBE形状,但是AD与BE的位置关系始终不变,请你帮他解释其中的原因.


【考点】反比例函数综合题.
【分析】(1)若四边形ADBE为菱形,则AB与DE互相垂直平分,则B和D的坐标可求得,然后利用待定系数法求得直线BC的解析式,进而求得C的坐标;
(2)设D的坐标是(a,﹣
 ),利用利用待定系数法即可求利用a表示出AD和BE的解析式,根据直线平行的条件即可判断.
),利用利用待定系数法即可求利用a表示出AD和BE的解析式,根据直线平行的条件即可判断.
【解答】解:(1)若四边形ADBE为菱形,则AB与DE互相垂直平分,
由题意得,A(﹣2,2),B(0,2).
则反比例函数的解析式是y=﹣
 ,E(﹣1,0)D(﹣1,4).
,E(﹣1,0)D(﹣1,4).
设直线BD的解析式是y=kx+b,
将B(0,2),D(﹣1,4)代入y=kx+b,可得: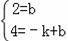
 ,
,
解得: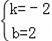
 ,
,
则直线BD的解析式是y=﹣2x+2,
所以C的坐标是(1,0);
(2)设D的坐标是(a,﹣
 ),直线AD的解析式是y=kx+b,则E(a,0).
),直线AD的解析式是y=kx+b,则E(a,0).
将A(﹣2,2),D(a,﹣
 )代入可得:
)代入可得:
 ,
,
解得:
 ,
,
则直线AD的解析式是y=﹣
 x+(2﹣
x+(2﹣
 ).
).
同理可得直线BE的解析式是y=﹣
 x+2,
x+2,
∴AD和BE始终平行.
【点评】本题考查了待定系数法求一次函数和直线的解析式,正确利用a表示出AD和BE的解析式是解决本题的关键.


科目:初中数学 来源: 题型:
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )


A.ab>0 B.a+b>0 C.(a﹣1)(b﹣1)>0 D.(a+1)(b﹣1)>0
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线AB外一点M,作一直线垂直于直线AB”,各自提供了如下四种方案,其中正确的是( )


A.甲、乙 B.乙、丙 C.丙、丁 D.甲、乙、丙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com