
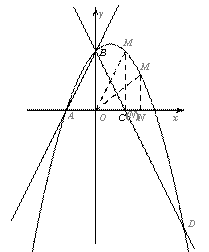
如图,直线y=2x+2与x轴交于点A,与y轴交于点B.把△AOB沿y 轴翻折,点A落到点C,过点B的抛物线
轴翻折,点A落到点C,过点B的抛物线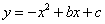 与直线BC交于点D(3,
与直线BC交于点D(3,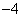 ).
).
(1)求直线BD和抛物线的解析式;
(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;
(3)在直线BD上方的抛物线上有一动点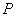 ,过点
,过点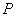 作PH垂直于x轴,交直线BD于点
作PH垂直于x轴,交直线BD于点 .当四边形
.当四边形 是平行四边形时,试求动点
是平行四边形时,试求动点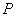 的坐标.
的坐标.
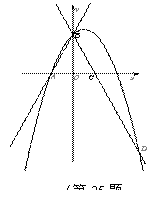
解:(1)在直线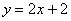 中,令
中,令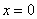 得
得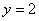 ,所以得点B
,所以得点B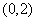
设直线BD的解析式为: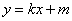 ,
,
代入B、D两点坐标得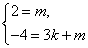
解得: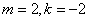 .
.
所以直线BD的解析式为: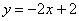 .
.
将B、D两点坐标代入抛物线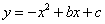 中得:
中得: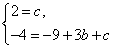
解得: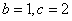 .
.
所以,抛物线的解析式为: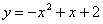
 (2)存在.
(2)存在.
假设存在点M(x,y)符合题意,则有如下两种情形:
①若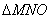 ∽
∽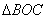 ,则
,则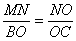 ,所以有
,所以有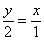 ,
,
即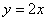 又因为M点在抛物线上所以
又因为M点在抛物线上所以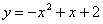 ,
,
所以: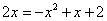
即: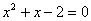
解得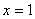 或
或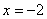 ,
,
又因为M点在第一象限,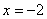 不符合题意,
不符合题意,
所以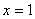 ,
,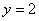 故M
故M .
.
②若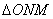 ∽
∽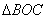 ,
,
则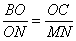 即
即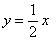 ,
,
所以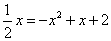
即: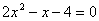
解得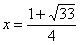 或
或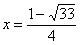 ,
,
又因为M点在第一象限,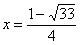 不符合题意,
不符合题意,
所以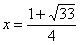 ,
,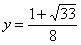 故M(
故M(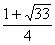 ,
,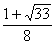 )…
)…
所以,符合条件的点M的坐标为 ,(
,(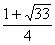 ,
,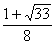 )
)
(3)设点P坐标为 则
则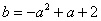
又因为点P在直线BD上方,
所以0<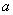 <3,
<3,
又PH 垂直于x轴,交直线BD于点 ,
,
所以H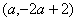 ,
,
所以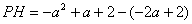
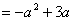 ,
,
因为四边形 是平行四边形,
是平行四边形,
所以PH=OB=2,
即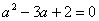 ,
,
解得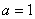 或
或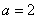 均满足0<
均满足0<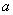 <3
<3
当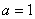 时,
时,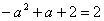 ,
,
当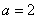 时,
时,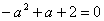 ,
,
所以点P的坐标为 ,
, 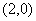


科目:初中数学 来源: 题型:
《1)如图1, Rt△ABC中,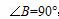 , AB= 2BC.现以C为圆心、CB为半径画弧交赵AC于D,再以
, AB= 2BC.现以C为圆心、CB为半径画弧交赵AC于D,再以
A为圆心,AD长为半径画弧交边AB于E.
求证: 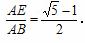 《这个比值
《这个比值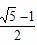 叫做AE与AB的黄金比·》
叫做AE与AB的黄金比·》
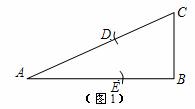
(2)如果一等睡三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请以
以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.(注:直尺没有刻度!作图不耍求
写作法,但要保留作图艘迹,并对作图中涉及的点用字母进行标注.)

查看答案和解析>>
科目:初中数学 来源: 题型:
东营市某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
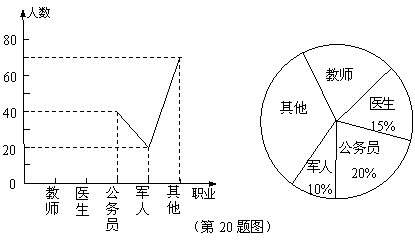 |
(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)求出扇形统计图中,公务员部分对应的圆心角的度数;
(4)若从被调查的学生中任意抽取一名,求抽取的这名学生最喜欢的职业是“教师”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
在某中学举行的演讲比赛中,初一年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差( )
| 选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 平均成绩 |
| 得分 | 90 | 95 | █ | 89 | 88 | 91 |
|
| A. | 2 | B. | 6.8 | C. | 34 | D. | 93 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2014的纵坐标为( )

|
| A. | 0 | B. | ﹣3×( | C. | (2 | D. | 3×( |
查看答案和解析>>
科目:初中数学 来源: 题型:
某“爱心义卖”活动中,购进甲、乙两种文具,甲每个进货价高于乙进货价10元,90元买乙的数量与150元买甲的数量相同。
(1)求甲、乙进货价;
(2)甲、乙共100件,将进价提高20%进行销售,进货价少于2080元,销售额要大于2460元,求有几种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com