
����Ŀ����ͼ1����ABCD�У�DH��AB�ڵ�H��CD�Ĵ�ֱƽ���߽�CD�ڵ�E����AB�ڵ�F��AB=6��DH=4��BF��FA=1��5��
��1����ͼ2����FG��AD�ڵ�G����DH�ڵ�M������DGM��DC����ƽ�ƣ��õ���CG��M��������M��B��
�����ı���BHMM���������
��ֱ��EF����һ����N������DNM�ܳ�����Сֵ��
��2����ͼ3���ӳ�CB��EF�ڵ�Q������Q��QK��AB����CD���ϵĶ���P��PK��EF������QK���ڵ�K������PKQ��ֱ��PQ���ۣ�ʹ��K�Ķ�Ӧ��K��ǡ������ֱ��AB�ϣ����߶�CP�ij���



���𰸡���1�����ı���BHMM�������Ϊ7.5������DNM�ܳ�����СֵΪ9����2��CP�ij�Ϊ![]() ��
��![]() ��
��
����������1���ٸ������������ε��ж��������Լ�ƽ�Ƶ����ʽ��н�ɣ�
������CM��ֱ��EF�ڵ�N������DN�����ù��ɶ�����ɣ�
��2���ֵ�P���߶�CE�Ϻ͵�P���߶�ED������������н��
��1������ABCD�У�AB=6��ֱ��EF��ֱƽ��CD��
��DE=FH=3��
��BF��FA=1��5��
��AH=2��
��Rt��AHD��Rt��MHF��
��![]() ��
��
��![]() ��
��
��HM=1.5��
����ƽ�Ƶ����ʣ�MM'=CD=6������BM����ͼ1��
�ı���BHMM�������=![]() =7.5��
=7.5��

������CM��ֱ��EF�ڵ�N������DN����ͼ2��

��ֱ��EF��ֱƽ��CD��
��CN=DN��
��MH=1.5��
��DM=2.5��
��Rt��CDM��MC2=DC2+DM2��
��MC2=62+��2.5��2��
��MC=6.5��
��MN+DN=MN+CN=MC��
���DNM�ܳ�����СֵΪ9��
��2����BF��CE��
��![]() ��
��
��QF=2��
��PK=PK'=6��
����K'��E'F'��EF���ֱ�CD�ڵ�E'����QK�ڵ�F'����ͼ3��

����P���߶�CE��ʱ��
��Rt��PK'E'��
PE'2=PK'2��E'K'2��
��PE��=2![]() ��
��
��Rt��PE'K'��Rt��K'F'Q��
��![]() ��
��
��![]() ��
��
��ã�QF��=![]() ��
��
��PE=PE'��EE'=![]() ��
��
��CP=![]() ��
��
ͬ���ɵã�����P���߶�DE��ʱ��CP��=![]() ������ͼ4��
������ͼ4��

����������CP�ij�Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����AB=4cm��AC��AB��BD��AB��AC=BD=3cm����P���߶�AB����1cm/s���ٶ��ɵ�A���B�˶���ͬʱ����Q���߶�BD���ɵ�B���D�˶������ǵ��˶�ʱ��Ϊt(s).

��1������Q���˶��ٶ����P���˶��ٶ���ȣ���t=1ʱ����ACP����BPQ�Ƿ�ȫ�ȣ���˵������
��2���жϴ�ʱ�߶�PC���߶�PQ�Ĺ�ϵ����˵�����ɡ�
��3����ͼ��2������ͼ��1���еġ�AC��AB��BD��AB����Ϊ����CAB=��DBA=60�����������������䣬���Q���˶��ٶ�Ϊx cm/s���Ƿ����ʵ��x��ʹ����ACP����BPQȫ�ȣ������ڣ������Ӧ��x��t��ֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�͡�ACB��ƽ�����ཻ�ڵ�F������F��DE��BC����AB��D����AC��E�����н�����ȷ���ǣ�������
��BD��CE����BDF����CEF���ǵ�����������BD+CE��DE����ADE���ܳ�ΪAB+AC��
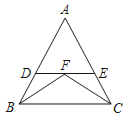
A.�٢�B.�ۢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��μ�һ��������������a��b��c���⣬ÿ����ߵ����ֻ��ߵ�0�֣�������a����20�֣���b����c���־�Ϊ25�֣����������ÿ��ѧ�����ٴ����һ�⣬����ȫ��Ե���1�ˣ�����������������15�ˣ������a������������b������֮��Ϊ29�������a������������c������֮��Ϊ25�������b������������c������֮��Ϊ20����������ƽ���ɼ���__�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳���ۺ�ʵ������ϣ�ͬѧ��Χ�ơ���֪���������ߵij��ȣ��������ε��������չ�������С��ͬѧ�뵽��������������������
��������ͼ��1����ͼ��2������6��6������������ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㣬�������֣�����С��ͬѧ��ͼ��1���л�����ABC���䶥��A��B��C���ڸ���ϣ�ͬʱ���쳤����CDEF��ʹ���Ķ��㶼�ڸ���ϣ������ı�EF������A��ED������B��ͬѧ�ǽ�����ͼ����ˡ�ABC�������
��1����ͼ��1���У���ABC�����߳��ֱ���AB���� ����BC���� ����AC���� ������ABC��������� ����
��2����֪��PMN�У�PM��![]() ��MN��2
��MN��2![]() ��NP��
��NP��![]() �������������С���˼·����ͼ��2���л�����PMN����ֱ��д����RMN������� ����
�������������С���˼·����ͼ��2���л�����PMN����ֱ��д����RMN������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ�����װ��30������ɫ����������ͬ�������к�����m����������3m����������Ϊ������С��Ӻ������������һ�������Ǻ�����С���ʤ��С�����������Żغ�����ҡ�ȣ���С���������һ������Ϊ������С����ʤ��
��1����m=4ʱ����С����������ĸ����Ƕ��٣�
��2����mΪ��ֵʱ����Ϸ��˫���ǹ�ƽ�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1���� Rt��ABC �У���ACB��90����AC��BC��D �� BC �ϵ�һ�㣬���� D �� DE��AB������Ϊ�� E��F Ϊ AD ���е㣬���� CF��EF��

��1������CF��EF�Ĺ�ϵ����˵�����ɣ�
��2����ͼ2������BF������AEF��30�������BFE �Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��

![]() ��֤���ı���
��֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
![]() ���ı���
���ı���![]() ������ʱ����
������ʱ����![]() �ij���
�ij���
![]() ���ı���
���ı���![]() �Ǿ���ʱ�����ʱ��
�Ǿ���ʱ�����ʱ��![]() ����
����![]() �ľ��룮
�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�����ɴ�С����״��ͬ�ġ�С�ȱ������Ρ�����һ���Ĺ�����ɣ����е�1��ͼ����3��С�ȱ������Σ���2��ͼ����8��С�������Σ���3��ͼ����15��С�ȱ������Σ��������ƣ����10��ͼ���У���������С�ȱ������Σ�

A.63B.80C.99D.120
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com