
【题目】有两个![]() 与
与![]() ,
,![]() 保持不动,且
保持不动,且![]() 的一边
的一边![]() ,另一边DE与直线OB相交于点F.
,另一边DE与直线OB相交于点F.
![]() 若
若![]() ,
,![]() ,解答下列问题:
,解答下列问题:
![]() 如图,当点E、O、D在同一条直线上,即点O与点F重合,则
如图,当点E、O、D在同一条直线上,即点O与点F重合,则![]() ______;
______;
![]() 当点E、O、D不在同一条直线上,画出图形并求
当点E、O、D不在同一条直线上,画出图形并求![]() 的度数;
的度数;
![]() 在
在![]() 的前提下,若
的前提下,若![]() ,
,![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的度数
的度数![]() 用含
用含![]() 、
、![]() 的式子表示
的式子表示![]() .
.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题:
(1)在被调查的学生中,喜欢“动画”节目的学生有 (名);
(2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 (度).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)设P(x,y),PD的长度为l,求l与x的函数关系式,并求l的最大值;
(3)当△ADP是直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,![]() 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为![]() .
.
![]() 填空:点A的坐标是______,点B的坐标是______;
填空:点A的坐标是______,点B的坐标是______;
![]() 将
将![]() 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到![]() 请写出
请写出![]() 的三个顶点坐标;
的三个顶点坐标;
![]() 求
求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,经过的点A(﹣4,0)、点B(6,0)的 抛物线与y轴相交于点C(0,m),连接BC.
(1)若△OAC∽△OCB,请求出m的值;
(2)当m=3时,试求出抛物线的解析式;
(3)在(2)的条件下,若P为抛物线上位于x轴上方的一动点,以P、A、B、C为顶点的四边形面积记作S,当S取何值时,相应的点P有且只有3个?
查看答案和解析>>
科目:初中数学 来源: 题型:
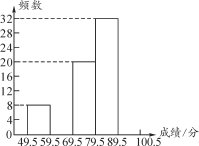
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数为1 000人.为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,最少为50分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
分组 | 频数 | 所占百分比 |
49.5~59.5 | 8 | 8% |
59.5~69.5 | __ __ | 12% |
69.5~79.5 | 20 | __ __ |
79.5~89.5 | 32 | __ __ |
89.5~100.5 | __ __ | 28% |
(1)补全频数分布表和频数分布直方图;
(2)若成绩在80分以上为优秀,求这次参赛的学生中成绩为优秀的约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com