
【题目】如图所示,OE是∠AOD的平分线,OC是∠BOD的平分线.
(1)若∠AOB=130°,则∠COE是多少度?
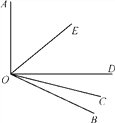
(2)在(1)的条件下,若∠COD=20°,则∠BOE是多少度?
【答案】(1) 65°(2) 85°
【解析】试题分析:(1)直接根据角平分线的定义进行解答即可;
(2)先根据∠COD=20°求出∠BOD的度数,再根据∠AOB=130°求出∠AOD的度数,根据角平分线的定义即可得出结论.
试题解析:(1)∵OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°
∴∠COE=![]() ∠BOD+
∠BOD+![]() ∠AOD=
∠AOD=![]() (∠BOD+∠AOD)=
(∠BOD+∠AOD)=![]() ∠AOB=65°;
∠AOB=65°;
(2)∵∠COD=20°,
∴∠BOD=2×20°=40°,
∵∠AOB=130°,
∴∠AOD=∠AOB-∠BOD=130°-40°=90°,
∵OE是∠BOD的平分线,
∴∠BOE=![]() ∠AOD+∠BOD=
∠AOD+∠BOD=![]() ×90°+40°=85°.
×90°+40°=85°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
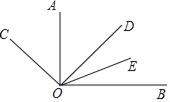
A. 113° B. 134° C. 136° D. 144°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
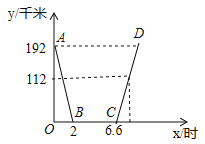
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( ) 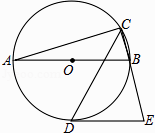
A.![]()
B.2
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2016年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量的说法错误的是( )
A.中位数是50
B.众数是51
C.平均数是46.8
D.方差是42
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com