
【题目】已知关于x的一元二次方程x2﹣2x +m+3=0,有两个实数根![]() ,
,![]()
(1)求m的取值范围。
(2)若![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值。
的值。
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.

(1)求一次函数y=k1x+b与反比例函数y=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
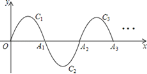
【题目】如图,一段抛物线:![]() (0≤x≤2)记为C1,它与x轴交于两点O、A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C7,若点P(13,m)在第7段抛物线C7上,则m=_____.
(0≤x≤2)记为C1,它与x轴交于两点O、A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C7,若点P(13,m)在第7段抛物线C7上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
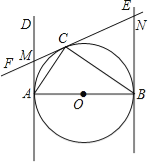
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车油箱的容积为![]() 升,小王把该车的油箱加满,从县城驾驶汽车到
升,小王把该车的油箱加满,从县城驾驶汽车到![]() 千米外的省城接客人,接到客人后立即按原路返回.请回答下列问题:
千米外的省城接客人,接到客人后立即按原路返回.请回答下列问题:
(1)油箱加满后,汽车能够行驶的总路程![]() (单位:千米)与平均耗油量
(单位:千米)与平均耗油量![]() (单位:升/千米)之间有怎样的函数关系?
(单位:升/千米)之间有怎样的函数关系?
(2)小王驾驶汽车去省城,平均每千米耗油![]() 升.返程时由于下雨,小王降低了车速,此时平均耗油量增加了一倍.小王不加油能否驾车回到县城?如果不能,至少还需加多少油才能保证回到县城?
升.返程时由于下雨,小王降低了车速,此时平均耗油量增加了一倍.小王不加油能否驾车回到县城?如果不能,至少还需加多少油才能保证回到县城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:![]() ,
,![]() ,精确到0.1m.)
,精确到0.1m.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
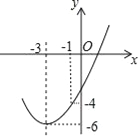
A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com