
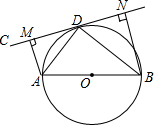
 如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.
如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.分析 (1)连接OD,由切线的性质和圆周角定理即可得到结果;
(2)由已知条件证得△ADM∽△ABD,即可得到结论;
(3)根据三角函数和勾股定理代入数值即可得到结果.
解答 (1)证明:连接OD,
∵直线CD切⊙O于点D,
∴∠CDO=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∵OB=OD,
∴∠3=∠4,
∴∠ADC=∠ABD;
(2)证明:∵AM⊥CD,
∴∠AMD=∠ADB=90°,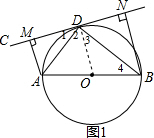
∵∠1=∠4,
∴△ADM∽△ABD,
∴$\frac{AM}{AD}=\frac{AD}{AB}$,
∴AD2=AM•AB;
(3)解:∵sin∠ABD=$\frac{3}{5}$,
∴sin∠1=$\frac{3}{5}$,
∵AM=$\frac{18}{5}$,
∴AD=6,
∴AB=10,
∴BD=$\sqrt{{AB}^{2}{-AD}^{2}}$=8,
∵BN⊥CD,
∴∠BND=90°,
∴∠DBN+∠BDN=∠1+∠BDN=90°,
∴∠DBN=∠1,
∴sin∠NBD=$\frac{3}{5}$,
∴DN=$\frac{24}{5}$,
∴BN=$\sqrt{{BD}^{2}{-DN}^{2}}$=$\frac{32}{5}$.
点评 本题考查了圆的切线性质,等腰三角形的性质,圆周角定理,解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:选择题
| A. | x+y=18 | B. | x+y=36 | C. | 4x+2y=36 | D. | 2x+4y=36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(min) | 0 | 3 | 6 | 8 | 12 | … |
| y(m) | 5 | 70 | 5 | 54 | 5 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
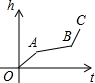 匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )| A. |  | B. |  | C. |  | D. | 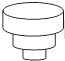 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com