
【题目】在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片![]() 沿过点
沿过点![]() 的直线折叠,使得点
的直线折叠,使得点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ;再将
;再将![]() 分别沿
分别沿![]() 折叠,此时点
折叠,此时点![]() 落在
落在![]() 上的同一点
上的同一点![]() 处.请完成下列探究:
处.请完成下列探究:
![]() 的大小为__________
的大小为__________![]() ;
;
![]() 当四边形
当四边形![]() 是平行四边形时
是平行四边形时![]() 的值为__________.
的值为__________.

【答案】30 ![]()
【解析】
(1)根据折叠得到∠D+∠C=180°,推出AD∥BC,,进而得到∠AQP=90°,以及∠A=180°-∠B=90°,再由折叠,得到∠DAQ=∠BAP=∠PAQ=30°即可;
(2)根据题意得到DC∥AP,从而证明∠APQ=∠PQR,得到QR=PR和QR=AR,结合(1)中结论,设QR=a,则AP=2a,由勾股定理表达出AB=AQ=![]() 即可解答.
即可解答.
解:(1)由题意可知,∠D+∠C=180°,
∴AD∥BC,
由折叠可知∠AQD=∠AQR,∠CQP=∠PQR,
∴∠AQR+∠PQR=![]() ,即∠AQP=90°,
,即∠AQP=90°,
∴∠B=90°,则∠A=180°-∠B=90°,
由折叠可知,∠DAQ=∠BAP=∠PAQ,
∴∠DAQ=∠BAP=∠PAQ=30°,
故答案为:30;
(2)若四边形APCD为平行四边形,则DC∥AP,
∴∠CQP=∠APQ,
由折叠可知:∠CQP=∠PQR,
∴∠APQ=∠PQR,
∴QR=PR,
同理可得:QR=AR,即R为AP的中点,
由(1)可知,∠AQP=90°,∠PAQ=30°,且AB=AQ,
设QR=a,则AP=2a,
∴QP=![]() ,
,
∴AB=AQ=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),直线
在第一象限),直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点.当这两条直线互相垂直,且四边形
两点.当这两条直线互相垂直,且四边形![]() 的周长为
的周长为![]() 时,点
时,点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(教材呈现)
下图是华师版九年级上册数学教材第79页的部分内容.
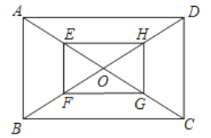
如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为__________;
的面积为__________;
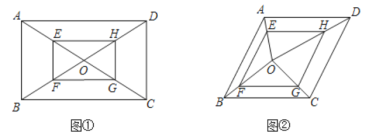
(2)如图②,在菱形![]() 中,
中,![]() ,
,![]() 是其内任意一点,连接
是其内任意一点,连接![]() 与菱形
与菱形![]() 各顶点,四边形
各顶点,四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,
上,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与
与![]() 的面积和为
的面积和为![]() ,则菱形
,则菱形![]() 的周长为___________.
的周长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
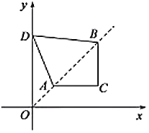
【题目】如图,在直角坐标系中,点![]() ,
,![]() 是第一象限角平分线上的两点,点
是第一象限角平分线上的两点,点![]() 的纵坐标为1,且
的纵坐标为1,且![]() ,在
,在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,使得四边形
,使得四边形![]() 的周长最小,这个最小周长的值为________.
的周长最小,这个最小周长的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣6,0),点B(0,8),点C在线段AB上,点D在y轴上,将∠ABO沿直线CD翻折,使点B与点A重合.若点E在线段CD延长线上,且CE=5,点M在y轴上,点N在坐标平面内,如果以点C、E、M、N为顶点的四边形是菱形,那么点N有( )
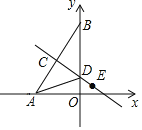
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
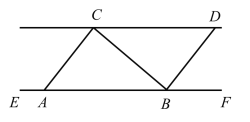
【题目】如图,为了测量某条河的对岸边C,D两点间的距离,在河的岸边与![]() 平行的直线
平行的直线![]() 上取两点A,B,测得
上取两点A,B,测得![]() ,
,![]()
![]() ,量得
,量得![]() 长为70米.求C,D两点间的距离(参考数据:
长为70米.求C,D两点间的距离(参考数据:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB是直线y=x+1的一部分,其中点A在y轴上,点B横坐标为2,曲线BC是双曲线![]() (
(![]() )的一部分,由点C开始不断重复“ABC”的过程,形成一组波浪线,点P(2019,m)与Q(2025,n)均在该波浪线上,G为x轴上一动点,则△PQG周长的最小值为( )
)的一部分,由点C开始不断重复“ABC”的过程,形成一组波浪线,点P(2019,m)与Q(2025,n)均在该波浪线上,G为x轴上一动点,则△PQG周长的最小值为( )

A.16B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com