
【题目】已知:在![]() 中,
中,![]() .
.
(1)若![]() .
.
①如图1,点![]() 在
在![]() 内,求
内,求![]() 的度数;
的度数;
②如图2,点![]() 在
在![]() 外,求
外,求![]() 的度数;
的度数;
(2)如图3,若![]() ,点
,点![]() 在
在![]() 内,且
内,且![]() ,求
,求![]() 的长.
的长.

【答案】(1)①150°;②30°;(2)2
【解析】
(1)①根据等边三角形的判定可知![]() 是等边三角形,由旋转的性质得到△CDO为等边三角形,根据勾股定理的逆定理判断出△BOD为直角三角形,即可得出答案;
是等边三角形,由旋转的性质得到△CDO为等边三角形,根据勾股定理的逆定理判断出△BOD为直角三角形,即可得出答案;
②由旋转的性质得到△DAO是等边三角形,根据勾股定理的逆定理判断出△BOD为直角三角形,即可;
(2)作出△ABQ∽△ACP,判断出△AOQ为直角三角形,从而得到△BOQ为直角三角形,根据勾股定理计算即可.
解:(1)![]()
![]() 是等边三角形,
是等边三角形,
①如图 1,把![]() 绕着点
绕着点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 旋转到点
旋转到点![]() ,得到
,得到![]() ,连结
,连结![]() .
.
由旋转可知![]()
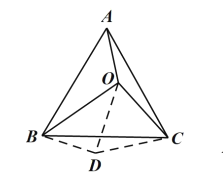
图1
![]()
![]() 为等边三角形
为等边三角形
![]()
![]()
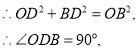
![]()
②如图 2, 把![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,得到
重合,得到![]() ,连接
,连接![]() .
.
![]()
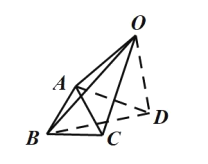
图2
![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
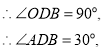
![]()
(2)如图3,作![]() ,使得:
,使得:![]()
则![]()
![]()
![]()
![]() 与
与![]() 相似比为
相似比为![]()
![]()
![]()
![]()
![]()
根据勾股定理得,![]()
![]() .
.
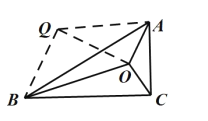
图3


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
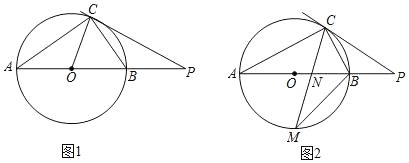
【题目】已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
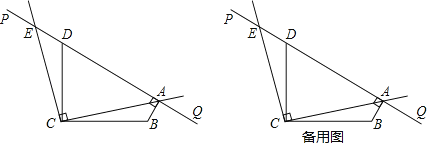
【题目】如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数 y=ax2+bx﹣(a+b)(a,b 是常数,a≠0).
(1)判断该二次函数图象与 x 轴的交点的个数,说明理由.
(2)若该二次函数图象经过 A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式.
(3)若 a+b<0,点 P(2,m)(m>0)在该二次函数图象上,求证:a>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
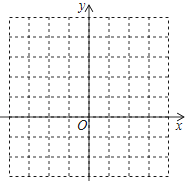
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年我校为确保学生安全,开展了“远离溺水珍爱生命”的防溺水安全知识竞赛.现从七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82 ;
八年级10名学生的竞赛成绩在C组中的数据是:92,90,94.
七、八年级抽取的学生竞赛成绩统计表

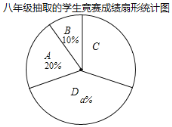
根据以上信息,解答下列问题:
(1)上述图表中a=______,b=______,c=______;
(2) 我校七、八年级共400人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生体育测试项目“400米跑”的训练情况,体育教师在2019年1-5月份期间,每月随机抽取部分学生进行测试,将测试成绩分为:A,B,C,D四个等级,并绘制如下两幅统计图.根据统计图提供的信息解答下列问题:

(1)______月份测试的学生人数最少,______月份测试的学生中男生、女生人数相等;
(2)求扇形统计图中D等级人数占5月份测试人数的百分比;
(3)若该校2019年5月份九年级在校学生有600名,请你估计出测试成绩是A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将函数![]() 为常数)的图象记为
为常数)的图象记为![]() 图象
图象![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() .
.
(1)若点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
(2)求![]() 的最小值;
的最小值;
(3)当直线![]() 的图象与函数
的图象与函数![]() 为常数)的图像只有一个公共点时,求
为常数)的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
(4)若![]() 点
点![]() 在图象
在图象![]() 上,且点
上,且点![]() 的横坐标为
的横坐标为![]() 点
点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .当点
.当点![]() 不在坐标轴上时,以点
不在坐标轴上时,以点![]() 为顶点构造矩形
为顶点构造矩形![]() 使点
使点![]() 落在
落在![]() 轴上.当图象
轴上.当图象![]() 与矩形
与矩形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片![]() 沿过点
沿过点![]() 的直线折叠,使得点
的直线折叠,使得点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ;再将
;再将![]() 分别沿
分别沿![]() 折叠,此时点
折叠,此时点![]() 落在
落在![]() 上的同一点
上的同一点![]() 处.请完成下列探究:
处.请完成下列探究:
![]() 的大小为__________
的大小为__________![]() ;
;
![]() 当四边形
当四边形![]() 是平行四边形时
是平行四边形时![]() 的值为__________.
的值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com