
分析 解方程得出x=2,再分母有理化,化简得出原式=4x+2,最后代入求出即可.
解答 解:$\frac{x-b}{a}$=2-$\frac{x-a}{b}$,
b(x-b)=2ab-a(x-a),
bx+ax=(a+b)2,
∵a+b=2,
∴2x=4,
∴x=2,
∴$\frac{\sqrt{x+1}-\sqrt{x}}{\sqrt{x+1}+\sqrt{x}}$+$\frac{\sqrt{x+1}+\sqrt{x}}{\sqrt{x+1}-\sqrt{x}}$
=$\frac{(\sqrt{x+1}-\sqrt{x})^{2}}{(\sqrt{x+1}+\sqrt{x})(\sqrt{x+1}-\sqrt{x})}$+$\frac{(\sqrt{x+1}+\sqrt{x})^{2}}{(\sqrt{x+1}-\sqrt{x})(\sqrt{x+1}+\sqrt{x})}$
=x+1-2$\sqrt{x(x+1)}$+x+x+1+2$\sqrt{x(x+1)}$+x
=4x+2
=4×2+2
=10.
点评 本题考查了分母有理化、解一元一次方程、二次根式的化简求出值等知识点,能正确分母有理化和求出x的值是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
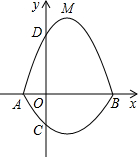 如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.
如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
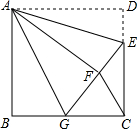 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com