
【题目】(1)计算:![]() ;
;
(2)先化简,再求值:![]() ,其中
,其中![]() ;
;
(3)解方程:![]() ;
;
(4)解不等式组: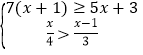 .
.
【答案】(1)![]() ;(2) x-1 ,
;(2) x-1 ,![]() ;(3)x=0 ;(4)-2≤x<4
;(3)x=0 ;(4)-2≤x<4
【解析】
(1)按实数混合运算法则进行计算.
(2)先把分式通分、因式分解再化简,然后进行计算.
(3)先确定最简共分母为(x+2)(x-2),再按分式方程的解法步骤计算,注意解完方程必须检验.
(4)分别计算两个不等式的解集,再求其公共解集.
(1)原式=![]() -1+(
-1+(![]() )2=6-1+
)2=6-1+![]() =5
=5![]() ;
;
(2)(x-![]() )÷
)÷![]() =
=![]() =
=![]() =x1
=x1
∵x=![]()
∴原式=![]() -1=
-1=![]()
(3)![]()
两边同时乘以(x+2)(x-2),得:
4+(x+2)(x-2)=x(x+2)
4+x2-4=x2+2x
2x=0
x=0
检验:当x=0时,(x+2)(x-2)≠0
∴原方程的解为x=0
(4)解不等式①:7(x+1)≥5x+3
7x+7≥5x+3
7x-5x≥3-7
2x≥-4
x≥-2
解不等式②:![]()
3x>4(x-1)
3x>4x-4
3x-4x>-4
x<4
∴不等式组的解集为-2≤x<4


科目:初中数学 来源: 题型:
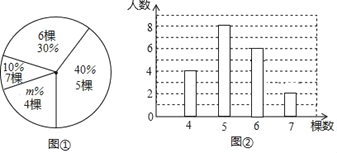
【题目】某校260名学生参加植树活动,活动结束后学校随机调查了部分学生每人的植树棵数,并绘制成如下的统计图①和统计图②.请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的学生人数为______,图①中m的值为_______;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)求本次调查获取的样本数据的平均数,并根据样本数据,估计这260名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.
(1)从口袋中随机摸出一个小球,小球上的数字是偶数的概率是______.
(2)从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
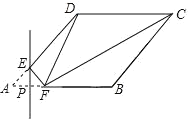
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
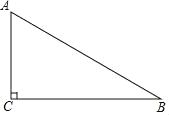
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连接AP,若AP平分∠CAB,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
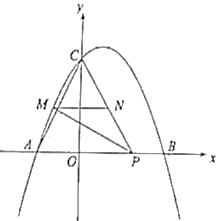
【题目】如图,已知抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)点A的坐标为_____,点C的坐标为______;
(2)如图,点M在抛物线![]() 位于A、C两点间的部分(与A、C两点不重合),过点M作PM⊥AC,与x轴正半轴交于点P,连接PC,过点M作MN平行于x轴,交PC于点N.
位于A、C两点间的部分(与A、C两点不重合),过点M作PM⊥AC,与x轴正半轴交于点P,连接PC,过点M作MN平行于x轴,交PC于点N.
①若点N为PC的中点,求出PM的长;
②当MN=NP时,求PC的长以及点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件.下列添加的条件中错误的是( )

A. ∠ACD=∠DAB B. AD=DE C. AD·AB=CD·BD D. AD2=BD·CD
查看答案和解析>>
科目:初中数学 来源: 题型:
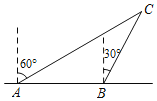
【题目】如图所示,一艘轮船在近海处由西向东航行,点C处有一灯塔,灯塔附近30海里的圆形区域内有暗礁,轮船在A处测得灯塔在北偏东60°方向上,轮船又由A向东航行40海里到B处,测得灯塔在北偏东30°方向上.
(1)求轮船在B处时到灯塔C处的距离是多少?
(2)若轮船继续向东航行,有无触礁危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则![]() 的长为______(用含n,π的式子表示).
的长为______(用含n,π的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com