
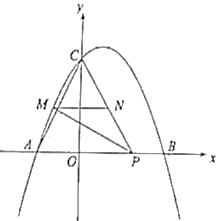
【题目】如图,已知抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)点A的坐标为_____,点C的坐标为______;
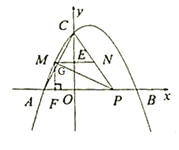
(2)如图,点M在抛物线![]() 位于A、C两点间的部分(与A、C两点不重合),过点M作PM⊥AC,与x轴正半轴交于点P,连接PC,过点M作MN平行于x轴,交PC于点N.
位于A、C两点间的部分(与A、C两点不重合),过点M作PM⊥AC,与x轴正半轴交于点P,连接PC,过点M作MN平行于x轴,交PC于点N.
①若点N为PC的中点,求出PM的长;
②当MN=NP时,求PC的长以及点M的坐标.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②PC=5,点
,②PC=5,点![]() 的坐标为
的坐标为![]()
【解析】
(1)在抛物线的解析式中,分别令y=0和x=0,即可得出结论.
(2)设直线MN与y轴相交于点E.过M作MF⊥x轴,垂足为F.
①由N是CP的中点,MN平行于x轴,得到E为CO的中点,从而得出MF =2,令抛物线解析式中y=2,解方程即可得出M的坐标,易求直线AC的解析式为y=2x+4,,由MP⊥AC,可设直线MP为![]() ,把M的坐标代入得到b的值,从而得到直线MP的解析式,进而求出P的坐标,根据两点间的距离公式即可求出PM的值.
,把M的坐标代入得到b的值,从而得到直线MP的解析式,进而求出P的坐标,根据两点间的距离公式即可求出PM的值.
②设AC交MP于G.由平行线的性质和等腰三角形的性质可得∠NPM=∠MPA,进而得到△APG≌△CPG,根据全等三角形的性质得到AG=GC,AP=PC.设P(x,0),根据两点间的距离公式列方程,求出x的值,可得P的坐标,得到PC=PA=5.再由中点坐标公式得到G的坐标.求出直线PG的解析式,和抛物线的解析式联立组成方程组,解方程组即可得到M的坐标.
(1)在![]() 中,令y=0,得:
中,令y=0,得:![]() ,解得:x=-2或x=4,∴A(-2,0),B(4,0).令x=0,得:y=4,∴C(0,4).
,解得:x=-2或x=4,∴A(-2,0),B(4,0).令x=0,得:y=4,∴C(0,4).
(2)直线MN与y轴相交于点E.过M作MF⊥x轴,垂足为F.
①∵N是CP的中点,MN平行于x轴,∴E为CO的中点,∴MF=OE=![]() CO=2,∴
CO=2,∴![]() ,解得:x=
,解得:x=![]() 或x=
或x=![]() (舍去),∴M(
(舍去),∴M(![]() ,2),易求直线AC的解析式为y=2x+4.
,2),易求直线AC的解析式为y=2x+4.
∵MP⊥AC,∴直线MP为![]() ,把M(
,把M(![]() ,2)代入得:b=
,2)代入得:b=![]() ,∴直线MP的解析式为:
,∴直线MP的解析式为:![]() ,令y=0,得:x=
,令y=0,得:x=![]() ,∴P(
,∴P(![]() ,0),∴PM=
,0),∴PM=![]() .
.
②设AC交MP于G.
∵MN∥AB,∴∠NMP=∠MPA.
∵MN=NP,∴∠NMP=∠NPM,∴∠NPM=∠MPA.
∵PG=PG,∠PGA=∠PGC=90°,∴△APG≌△CPG,∴AG=GC,AP=PC.设P(x,0),∴![]() ,解得:x=3,∴P(3,0),∴PC=PA=3+2=5.
,解得:x=3,∴P(3,0),∴PC=PA=3+2=5.
∵AG=GC,∴G为AC的中点,∴G(-1,2).
设直线PG为y=kx+b,∴![]() ,解得:
,解得: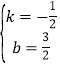 ,∴直线PG为
,∴直线PG为![]() .解方程组:
.解方程组: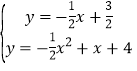 ,得:
,得: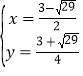 或
或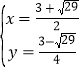 (舍去),∴点M的坐标为
(舍去),∴点M的坐标为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
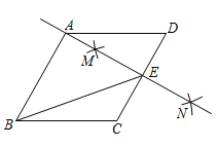
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
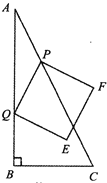
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点P从点A出发,以每秒
.点P从点A出发,以每秒![]() 个单位长度的速度向终点C运动.点Q从点B出发,以每秒2个单位长度的速度向终点A运动.连结PQ,将线段PQ绕点Q顺时针旋转
个单位长度的速度向终点C运动.点Q从点B出发,以每秒2个单位长度的速度向终点A运动.连结PQ,将线段PQ绕点Q顺时针旋转![]() 得到线段QE,以PQ、QE为边作正方形PQEF.设点P运动的时间为t秒
得到线段QE,以PQ、QE为边作正方形PQEF.设点P运动的时间为t秒![]() .
.
(1).点P到边AB的距离为______(用含t的代数式表示).
(2).当![]() 时,求t的值.
时,求t的值.
(3).连结BE.设![]() 的面积为S,求S与t之间的函数关系式.
的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富村民业余文化生活,某开发区某村民委员会动员村民自愿集资建立一个书、报、刊阅览室.经预算,一共需要筹资50000元,其中一部分用于购买桌、凳、柜等设施,另一部分用于购买书、报、刊.
(1)村委会计划,购买书、报、刊的资金不少于购买桌、凳、柜资金的4倍,问最多用多少资金购买桌、凳、柜等设施?
(2)经初步估计,有250户村民自愿参与集资,那么平均每户需集资200元.开发区管委会了解情况后,赠送了一批阅览室设施和书、报、刊.这样,只需参与户共集资36000元.经村委会进一步宣传,自愿参与的户数在250户的基础上增加了![]() (其中
(其中![]() ).则每户平均集资的资金在200元的基础上减少了
).则每户平均集资的资金在200元的基础上减少了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ∶S△ABC=9∶100?若存在,求出t的值;若不存在,说明理由;
(3)当t为何值时,△CPQ为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
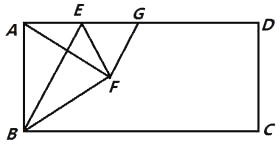
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com