
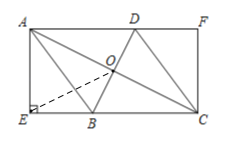
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若cos∠BAE=![]() ,AB=5,求OE的长.
,AB=5,求OE的长.

【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)根据菱形的性质得到AD∥BC,推出四边形AECF是平行四边形,根据矩形的判定定理即可得到结论;
(2)根据三角函数的定义得到AE=4,BE=3,根据勾股定理得到AC=4![]() ,再根据直角三角形斜边中线的性质即可得到结论.
,再根据直角三角形斜边中线的性质即可得到结论.
(1)∵四边形ABCD是菱形,
∴AD∥BC,
∵CF∥AE,
∴四边形AECF是平行四边形,
∵AE⊥BC,
∴四边形AECF是矩形;
(2)在Rt△ABE中,∠E=90°,∵cos∠BAE=![]() =
=![]() ,AB=5,
,AB=5,
∴AE=4,
∴BE=![]() =3,
=3,
∵AB=BC=5,
∴CE=8,
∴AC=![]() =4
=4![]() ,
,
∵四边形ABCD是菱形,AC、BD交于点O,
∴AO=CO,
∵∠AEC=90°,
∴OE=![]() AC=2
AC=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用两个月时间试销某种新型商品,经市场调查,该商品的第![]() 天的进价
天的进价![]() (元/件)与
(元/件)与![]() (天)之间的相关信息如下表:
(天)之间的相关信息如下表:
时间 |
|
|
进价 |
| 40 |
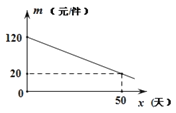
该商品在销售过程中,销售量![]() (件)与
(件)与![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
在销售过程中,商场每天销售的该产品以每件80元的价格全部售出.
(1)求该商品的销售量![]() (件)与
(件)与![]() (天)之间的函数关系;
(天)之间的函数关系;
(2)设第![]() 天该商场销售该商品获得的利润为
天该商场销售该商品获得的利润为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
(3)在销售过程中,当天的销售利润不低于2400元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
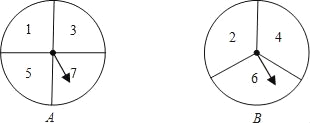
【题目】如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)计算点P在函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图像过点
的图像过点![]() ,顶点为
,顶点为![]()
![]() 求
求![]() 的值.
的值.
![]() 点
点![]() 以点
以点![]() 为旋转中心,顺时针旋转
为旋转中心,顺时针旋转![]() 得到点
得到点![]() ,判断点
,判断点![]() 是否落在抛物线上.
是否落在抛物线上.
![]() 第一象限内抛物线上有一点
第一象限内抛物线上有一点![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 时,求点
时,求点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣(2a+1)x+c(a>0)的图象经过坐标原点O,一次函数y=﹣x+4与x轴、y轴分别交于点A、B.
(1)c= ,点A的坐标为 ;
(2)若二次函数y=ax2﹣(2a+1)x+c的图象经过点A,求a的值;
(3)若二次函数y=ax2﹣(2a+1)x+c的图象与△AOB只有一个公共点,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决所提的问题:
勾股定理a+b=c本身就是一个关于a,b,c的方程,我们知道这个方程有无数组解,满足该方程的正整数解(a,b,c)通常叫做勾股数组.关于勾股数组的研究我国历史上有非常辉煌的成就,根据我国古代数学书《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三、股修四、径隅五”(古人把较短的直角边称为勾,较长的直角边称为股,而斜边则为弦),即知道了勾股数组(3,4,5).类似地,还可以得到下列勾股数组:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…等等,这些数组也叫做毕达哥拉斯勾股数组.
上述勾股数组的规律,可以用下面表格直观表示:
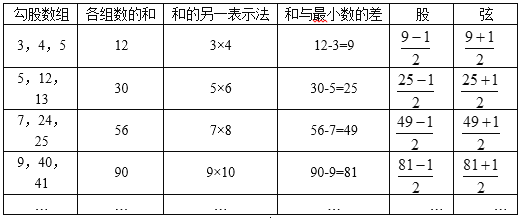
观察分析上述勾股数组,可以看出它们具有如下特点:
特点1:最小的勾股数的平方等于另两个勾股数的和;
特点2:____________________________________.
…
学习任务:
(1)请你再写出上述勾股数组的一个特点:________________;
(2)如果n表示比1大的奇数,则上述勾股数组可以表示为(n,______,______)
(3)请你证明(2)的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字-1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上.
(1)小明从这四张卡片中随机抽取一张, 抽到一张恰好是负数的概率是多少?
(2)随机抽出一张,记其数字为![]() ,不放回,再随机抽出一张, 记其数字为
,不放回,再随机抽出一张, 记其数字为![]() ,则使关于
,则使关于![]() 的方程
的方程![]() 有实数根的概率是多少?
有实数根的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com