【题目】如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A、B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m.
（1）求点B到AC的距离；
（2）求线段CD的长度.
【答案】(1)30m；(2)(15+15
)m
【解析】
试题分析：(1)、过点B作BE⊥AC于点E，根据Rt△AEB中∠A的正弦值得出BE的长度；(2)、根据题意得出AE的长度，然后求出AC的长度，最后根据Rt△ADC的三角函数得出CD的长度.
试题解析：(1)、过点B作BE⊥AC于点E，
在Rt△AEB中，AB=60m，sinA=
，BE=ABsinA=60×=30m，
(2)、cosA=
， ∴AE=60×
=30
m
在Rt△CEB中，∠ACB=∠CBD﹣∠A=75°﹣30°=45°，∴BE=CE=30m， ∴AC=AE+CE=（30+30
）m
在Rt△ADC中，sinA=
， 则CD=（30+30）×
=（15+15）m.
科目：初中数学 来源： 题型：
【题目】按图填空，并注明理由．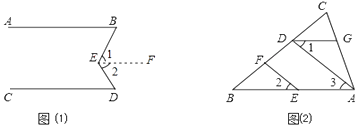 
（1）完成正确的证明：如图（1），已知AB∥CD，求证：∠BED=∠B+∠D
证明：过E点作EF∥AB（经过直线外一点有且只有一条直线与这条直线平行）
∴∠1=（）
∵AB∥CD（已知）
∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行）
∴∠2=（）
又∠BED=∠1+∠2
∴∠BED=∠B+∠D （等量代换）．
（2）如图（2），在△ABC中，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
解：因为EF∥AD（已知）
所以∠2=∠3．（）
又因为∠1=∠2，所以∠1=∠3．（等量代换）
所以AB∥（）
所以∠BAC+=180° （）．
又因为∠BAC=70°，所以∠AGD=110°．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面.
（1）请你补全这个输水管道的圆形截面；
（2）若这个输水管道有水部分的水面宽AB＝16cm，水面最深地方的高度为4cm，求这个圆形截面的半径.
查看答案和解析>>
科目：初中数学 来源： 题型：
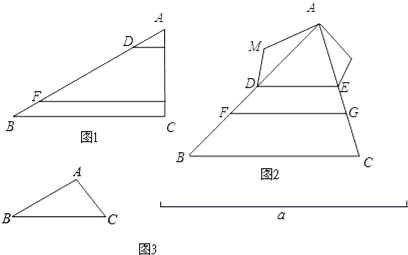
【题目】【回归课本】我们曾学习过一个基本事实：两条直线被一组平行线所截，所得的对应线段成比例．
【初步体验】
（1）如图1，在△ABC中，点D、F在AB上，E、G在AC上，DE∥FC∥BC．若AD=2，AE=1，DF=6，则EG= ， 
= ．
（2）如图2，在△ABC 中，点D、F在AB上，E、G在AC上，且DE∥BC∥FG．以AD、DF、FB为边构造△ADM（即AM=BF，MD=DF）；以AE、EG、GC为边构造△AEN（即AN=GC，NE=EG）．
求证：∠M=∠N．
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题：
（3）如图3，已知△ABC和线段a，请用直尺与圆规作△A′B′C′．
满足：①△A′B′C′∽△ABC；②△A′B′C′的周长等于线段a的长度．（保留作图痕迹，并写出作图步骤）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解方程：
（1）2（x+1）2=8；
（2）x2+2x+1=8（配方法）；
（3）2x2﹣3x﹣1=0 （公式法）；
（4）64（3y﹣2）2=9（2y﹣3）2
（5）（x﹣1）2﹣4（x﹣1）+4=0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点（﹣2，y1），（﹣1，y2），（1，y3）都在直线y=﹣3x+b上，则y1，y2，y3的值的大小关系是（ ）
A. y1＞y2＞y3 B. y1＜y2＜y3 C. y3＞y1＞y2 D. y3＜y1＜y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
