
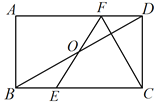
【题目】如图,点O为矩形ABCD对角线BD的中点,直线EF经过点O分别与边BC,AD交于点E, F,连接CF,若∠CEF=2∠CBD,∠CBD =30°,DC=![]() ,有下面的结论:①FD=BE;②∠EOD=150°;③BE2+AB2=AF2;④BC=6;⑤直线FC是线段OD的垂直平分线.其中正确的个数为( )个.
,有下面的结论:①FD=BE;②∠EOD=150°;③BE2+AB2=AF2;④BC=6;⑤直线FC是线段OD的垂直平分线.其中正确的个数为( )个.
A. 2B. 3C. 4D. 5
【答案】D
【解析】
根据矩形的性质易证△BOE≌△DOF,可得FD=BE,所以①正确;由∠CEF=∠CBO +∠BOE=2∠CBD,求出∠CBO =∠BOE=30°,可得∠EOD=150°,所以②正确;根据一组对边平行且相等的四边形是平行四边形证明四边形AECF是平行四边形,根据矩形的性质结合∠CBD =30°证明△OCD为等边三角形,求出∠EOC=90°可得平行四边形AECF是菱形,得到AE=AF,由勾股定理可得BE2+AB2=AF2,所以③正确;根据含30°直角三角形的性质可求出BC=6,故④正确;根据等角对等边得到FO=FD,根据等边三角形的性质得到CO=CD,可得直线FC是线段OD的垂直平分线,所以⑤正确.
解:∵AD∥BC,
∴∠FDO =∠EBO,
又∵∠FOD =∠EOB,OB=OD,
∴△BOE≌△DOF(ASA),
∴FD=BE,故①正确;
∵∠CEF=∠CBO +∠BOE=2∠CBD,
∴∠CBO =∠BOE=30°,
∴∠EOD=180°-30°=150°,故②正确;
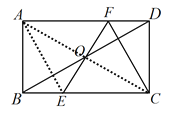
连结AE,AC,
∵FD=BE,
∴AF=EC,
∵AD∥BC,
∴四边形AECF是平行四边形,
∵∠CBD =30°,
∴∠BDC=60°,
∵OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴∠OCE=30°,
∵∠CEF=2∠CBD=60°,
∴∠EOC=90°,即AC⊥EF,
∴平行四边形AECF是菱形,
∴AE=AF,
∵BE2+AB2=AE2,
∴BE2+AB2=AF2,故③正确;
∵∠CBD =30°,DC=![]() ,∠BCD=90°,
,∠BCD=90°,
∴BC=![]() DC=6,故④正确;
DC=6,故④正确;
∵△BOE≌△DOF,
∴∠CBO =∠BOE=∠FDO =∠FOD,
∴FO=FD,
∵△OCD为等边三角形,
∴CO=CD,
∴直线FC是线段OD的垂直平分线,故⑤正确,
正确的有5个,
故选:D.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,计算
,计算![]() ,
,
![]() ,
,
![]() .
.
猜想:![]() (n为正整数);
(n为正整数);
(1)根据你的猜想计算:
①![]()
②![]() (n为正整数)
(n为正整数)
③![]()
(2)通过以上规律请你进行下面的探索:
①![]()
②![]()
③![]()
(3)判断![]() 的个位数字是
的个位数字是
查看答案和解析>>
科目:初中数学 来源: 题型:
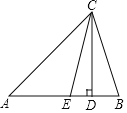
【题目】如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=40°,∠B=76°,求∠DCE的度数;
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示);
(3)当线段CD沿DA方向平移时,平移后的线段与线段CE交于G点,与AB交于H点,若∠A=α,∠B=β,求∠HGE与α、β的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬至过后,昼夜温差逐渐加大,山城的市民们已然感受到了深冬的寒意.在还未普遍使用地暖供暖设备的山城,小型电取暖器仍然深受市民的青睐.某格力专卖店销售壁挂式电暖器和卤素/石英式取暖器(俗称 “小太阳”),其中壁挂式电暖器的售价是“小太阳”售价的5倍还多100元,2016年12月份壁挂式电暖器和“小太阳”共销售500台,壁挂式电暖器与“小太阳”销量之比是4∶1,销售总收入为58.6万元.
(1)分别求出每台壁挂式电暖器和“小太阳”的售价;
(2)随着“元旦、春节”双节的来临和气温的回升,销售进入淡季,2017年1月份,壁挂式电暖器的售价比2016年12月下调了4m﹪,根据经验销售量将比2016年12月下滑6m﹪,而“小太阳”的销售量和售价都维持不变,预计销售总收入将下降到16.04万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年11月2日﹣4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
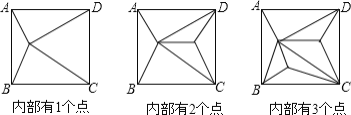
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC与三角形![]() 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形![]() 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.
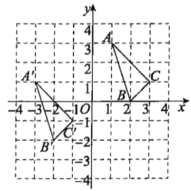
(1)分别写出点![]()
![]()
![]() 的坐标;
的坐标;
(2)说明三角形![]() 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;
(3)若点![]() 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形![]() 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.
A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com