
【题目】已知![]() ,计算
,计算![]() ,
,
![]() ,
,
![]() .
.
猜想:![]() (n为正整数);
(n为正整数);
(1)根据你的猜想计算:
①![]()
②![]() (n为正整数)
(n为正整数)
③![]()
(2)通过以上规律请你进行下面的探索:
①![]()
②![]()
③![]()
(3)判断![]() 的个位数字是
的个位数字是
【答案】猜想:![]() ;(1)①
;(1)①![]() ;②
;②![]() ;③
;③![]() ;(2)①
;(2)①![]() ;②
;②![]() ;③
;③![]() ;(3)5.
;(3)5.
【解析】
根据已知的式子,找出规律,即可得到猜想的结论;
(1)①根据猜想的结论,当![]() 时,即可得到答案;
时,即可得到答案;
②根据猜想的结论,当![]() 时,通过计算,即可得到答案;
时,通过计算,即可得到答案;
③根据猜想的结论,即可得到答案;
(2)根据(1)中的结论,即可得到答案;
(3)结合(1)(2)中的结论,通过变形化简,即可得到答案.
解:根据题意,有
![]() ;
;
故答案为:![]() ;
;
(1)①∵![]() ,
,
∴![]() ;
;
故答案为:![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为:![]() ;
;
③∵![]()
∴![]() ;
;
故答案为:![]() ;
;
(2)①![]() ;
;
②![]() ;
;
同理可知:
③![]() ;
;
(3)由(2)可知,
![]() ;
;
∴当![]() ,
,![]() ,
,![]() 时,有
时,有
![]() ,
,
∴![]() ;
;
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,……
,……
∴![]() 的个位数字是2、4、8、6,每4个数字一个循环;
的个位数字是2、4、8、6,每4个数字一个循环;
∵![]() ,
,
∴![]() 的个位上的数字是6;
的个位上的数字是6;
∴![]() 的个位上的数字是5;
的个位上的数字是5;
故答案为:5.


科目:初中数学 来源: 题型:
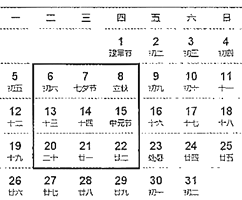
【题目】如图是某月的月历表,在此月历表上可以用一个矩形圈出![]() 个位置相邻的数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为_____.
个位置相邻的数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
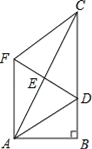
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
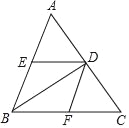
【题目】如图,在△ABC中,DF∥AB,DE∥BC,连接BD.
(1)求证:△DEB≌△BFD;
(2)若点D是AC边的中点,当△ABC满足条件_____时,四边形DEBF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
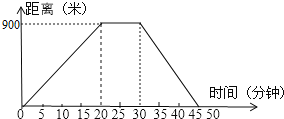
【题目】如图,反映了小明从家里到超市的时间与距离之间关系的一幅图。
(1)图中自变量和因变量各是什么?
(2)小明到达超市用了多少时间?超市离家多远?
(3)分别求小明从家里到超市时的平均速度是多少?返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为( )
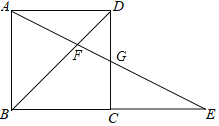
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学课上,老师要求学生根据图中李亮与张鑫的对话内容,展开如下活动:
仔细阅读对话内容:

活动:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,他需要付多少钱;
(2)你认为购买多少元钱的书时办卡与不办卡花费相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为矩形ABCD对角线BD的中点,直线EF经过点O分别与边BC,AD交于点E, F,连接CF,若∠CEF=2∠CBD,∠CBD =30°,DC=![]() ,有下面的结论:①FD=BE;②∠EOD=150°;③BE2+AB2=AF2;④BC=6;⑤直线FC是线段OD的垂直平分线.其中正确的个数为( )个.
,有下面的结论:①FD=BE;②∠EOD=150°;③BE2+AB2=AF2;④BC=6;⑤直线FC是线段OD的垂直平分线.其中正确的个数为( )个.
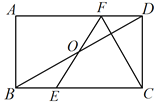
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com