
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定: (a,b)★(c,d)=bc-ad.例如:(1,2)★(3,4)=2×3-1×4=2.根据上述规定解决下列问题:
(1)有理数对(2,3)★(3,-2)= ;
(2)若有理数对(-3,2x-1)★(1,x+1)=12,则x= ;
(3)当满足等式(-3,2x-1)★(k,x+k)=3+2k的x是整数时,求整数k的值.
【答案】(1)13;(2)2;(3)k=0,-1,-2,-3
【解析】
(1)根据(a,b)★(c,d)=bc-ad,将相应式子代入,即可求解;
(2)根据(a,b)★(c,d)=bc-ad,将相应式子代入,可求出x的值;
(3)当满足等式(-3,2x-1)★(k,x+k)=3+2k时,将相应式子代入,可得![]() ,根据x是整数,得出3必须是2k+3的整数倍,依此进行求解.
,根据x是整数,得出3必须是2k+3的整数倍,依此进行求解.
(1)根据(a,b)★(c,d)=bc-ad,可得
(2,3)★(3,-2)=![]() ;
;
(2)若有理数对(-3,2x-1)★(1,x+1)=12,可得
![]() ,解得x=2;
,解得x=2;
(3)当满足等式(-3,2x-1)★(k,x+k)=3+2k时,
![]() ,解得:
,解得:![]()
∵x是整数,可得3一定是2k+3的倍数,即![]() ,解得
,解得![]() ,依次将k=0,-1,-2,-3带入可得x均为整数,故当k=0,-1,-2,-3时满足题意.
,依次将k=0,-1,-2,-3带入可得x均为整数,故当k=0,-1,-2,-3时满足题意.


科目:初中数学 来源: 题型:
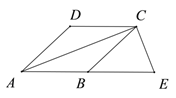
【题目】如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E.
(1)求证:CD=BE;
(2)如果∠E=60°,CE=m,请写出求菱形ABCD面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
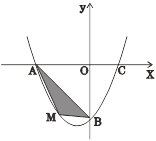
【题目】在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为![]() ,△AMB的面积为S.求S关于
,△AMB的面积为S.求S关于![]() 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
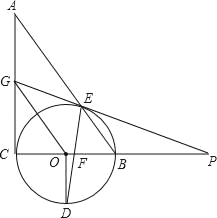
【题目】如图,Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列4个结论:①GE=GC;②AG=GE;③OG∥BE;④∠A=∠P.其中正确的结论是_____(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在数轴上的三个点![]() 、
、![]() ,
,![]() 表示的数分别为-3、-2、2,试回答下列问题:
表示的数分别为-3、-2、2,试回答下列问题:
![]()
(1)![]() ,
,![]() 两点间的距离是______;
两点间的距离是______;
(2)若![]() 点与
点与![]() 点的距离是8,则
点的距离是8,则![]() 点表示的数是多少?
点表示的数是多少?
(3)若将数轴折叠,使![]() 点与
点与![]() 点重合,则
点重合,则![]() 点与哪个数重合?
点与哪个数重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下面各数填入相应的大括号内.
-13.5,5,0,-10,-15%,![]()
负数集合:{ …},
非负数集合:{ …},
整数集合:{ …},
负分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com