
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
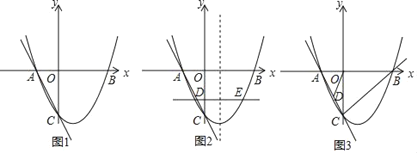
(1)求直线AC的解析式;
(2)如图2,点E(a,b)是对称轴右侧抛物线上一点,过点E垂直于y轴的直线与AC交于点D(m,n).点P是x轴上的一点,点Q是该抛物线对称轴上的一点,当a+m最大时,求点E的坐标,并直接写出EQ+PQ+![]() PB的最小值;
PB的最小值;
(3)如图3,在(2)的条件下,连结OD,将△AOD沿x轴翻折得到△AOM,再将△AOM沿射线CB的方向以每秒3个单位的速度沿平移,记平移后的△AOM为△A′O'M',同时抛物线以每秒1个单位的速度沿x轴正方向平移,点B的对应点为B'.△A'B'M'能否为等腰三角形?若能,请求出所有符合条件的点M'的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)E(3,
;(2)E(3,![]() ),点F(﹣1,
),点F(﹣1,![]() ),
),![]() ;(3)符合条件的点M'的坐标M′(0,
;(3)符合条件的点M'的坐标M′(0,![]() ).
).
【解析】
(1)y=![]() ,令y=0,x=0,求出A(﹣2,0)、B(4,0)、C(0,﹣2
,令y=0,x=0,求出A(﹣2,0)、B(4,0)、C(0,﹣2![]() ),把A、C坐标代入y=kx+b,即可求解;
),把A、C坐标代入y=kx+b,即可求解;
(2)①由n=b,解得:m=﹣![]() m2+
m2+![]() a,则a+m=a+(﹣
a,则a+m=a+(﹣![]() m2+
m2+![]() a)=﹣
a)=﹣![]() (a﹣3)2+
(a﹣3)2+![]() ,即可求解;②F是E关于对称轴的对称点,则在如图位置时,EQ+PQ=PF最小,即EQ+PQ+
,即可求解;②F是E关于对称轴的对称点,则在如图位置时,EQ+PQ=PF最小,即EQ+PQ+![]() PB是最小值,即可求解;
PB是最小值,即可求解;
(3)设移动的时间t秒,各点坐标为:A′(﹣2+2t)、B′(4+t)、M′(﹣![]() +2t,
+2t,![]() t),分AB′2=AM′2、AB′2=BM′2、BM′2=AM′2讨论求解.
t),分AB′2=AM′2、AB′2=BM′2、BM′2=AM′2讨论求解.
(1)y=![]() ,
,
令y=0,解得x=﹣2或4,令x=0,则y=﹣2![]() ,
,
∴点A(﹣2,0)、B(4,0)、C(0,﹣2![]() );
);
把A、C坐标代入y=kx+b,
解得:k=﹣![]() ,b=﹣2
,b=﹣2![]() ,
,
∴直线AC的解析式y=﹣![]() x﹣2
x﹣2![]() ;
;
(2)∵E(a,b)在抛物线上,∴b=![]() ,
,
∵D(m,n)在直线AC上,∴n=﹣![]() m﹣2
m﹣2![]() ,
,
∵DE⊥y轴,∴n=b,解得:m=﹣![]() a2+
a2+![]() a,
a,
∴a+m=a+(﹣![]() a2+
a2+![]() a)=﹣
a)=﹣![]() (a﹣3)2+
(a﹣3)2+![]() ,
,
∴当a=3时,a+m由最大值,b=![]() ,
,
则:E(3,![]() ),点F(﹣1,
),点F(﹣1,![]() ),
),
如下图2所示,连接BC,过点F作FP∥BC,交对称轴和x轴于点Q、P,
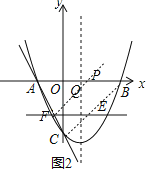
∵F是E关于对称轴的对称点,则在如图位置时,EQ+PQ=PF最小,即EQ+PQ+![]() PB是最小值,
PB是最小值,
kBC=![]() =kFP,把kFP和点F坐标代入y=kx+b,
=kFP,把kFP和点F坐标代入y=kx+b,
解得:b=﹣![]() ,即:y=
,即:y=![]() x﹣
x﹣![]() ,
,
令y=0,则x=![]() ,即点P(
,即点P(![]() ,0),
,0),
则PF=![]() ,而
,而![]() PB=
PB=![]() (4﹣
(4﹣![]() )=
)=![]() ,
,
EQ+PQ+![]() PB=PF+
PB=PF+![]() PB=
PB=![]() ;
;
故:点E坐标为(3,![]() ),EQ+PQ+
),EQ+PQ+![]() PB的最小值为
PB的最小值为![]() ;
;
(3)设移动的时间t秒,△A′O′M′移动到如图所示的位置,
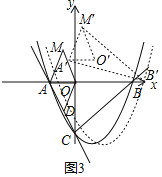
则此时各点坐标为:A′(﹣2+2t)、B′(4+t)、M′(﹣![]() +2t,
+2t,![]() +
+![]() t),
t),
则AB′2=6t2﹣12t+36,AM′2=![]() ,BM′2=6t2+3t+
,BM′2=6t2+3t+![]() ,
,
当AB′2=AM′2时,6t2﹣12t+36=![]() ,方程无解,
,方程无解,
当AB′2=BM′2时,6t2﹣12t+36=6t2+3t+![]() ,t=
,t=![]() ,M′(0,
,M′(0,![]() ),
),
当BM′2=AM′2时,6t2+3t+![]() =
=![]() ,方程无解,
,方程无解,
故:符合条件的点M'的坐标M′(0,![]() ).
).


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
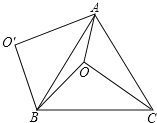
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O'的距离为8;③四边形AOBO'的面积为24+15![]() ; ④∠AOB=150°;⑤s△AOC+S△AOB=9
; ④∠AOB=150°;⑤s△AOC+S△AOB=9![]() +24,其中正确的结论是_____.
+24,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
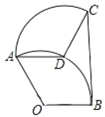
【题目】如图,将半径为1,圆心角为120°的扇形OAB绕点A逆时针旋转一个角度,使点O的对应点D落在弧AB上,点B的对应点为C,连接BC,则图中CD、BC和弧BD围成的封闭图形面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,有![]() ,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
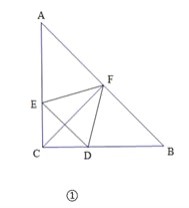
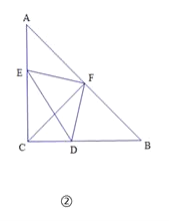
(1)已知点F是AB的中点.
①如图①,若△DEF是等边三角形,试直接写出正△DEF的边长;
②如图②,若![]() , △DEF 的面积为10,求CD的长;
, △DEF 的面积为10,求CD的长;
(2)若![]() ,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
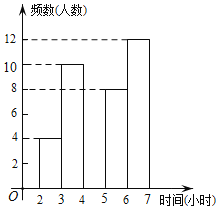
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com