
【题目】在△ABC中,有![]() ,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
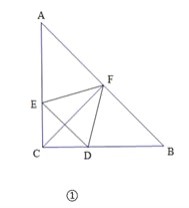
(1)已知点F是AB的中点.
①如图①,若△DEF是等边三角形,试直接写出正△DEF的边长;
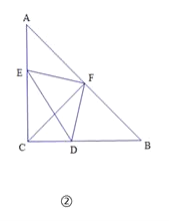
②如图②,若![]() , △DEF 的面积为10,求CD的长;
, △DEF 的面积为10,求CD的长;
(2)若![]() ,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
【答案】(1)①![]() ;②CD=2或6;(2)
;②CD=2或6;(2)![]()
【解析】
(1)①作FG⊥BC交BC于点G,由题可得:CF垂直平分DE、AB,设CE=CD=a,由勾股定理得DE=DF=![]() a,根据 等腰直角三角形性质得CG=BG=FG=4,DG=4-a,在Rt△FGD中,由勾股定理得一元二次方程,解之可得a值,从而可得等边三角形△DEF边长;
a,根据 等腰直角三角形性质得CG=BG=FG=4,DG=4-a,在Rt△FGD中,由勾股定理得一元二次方程,解之可得a值,从而可得等边三角形△DEF边长;
②根据等腰直角三角形性质和等量代换得∠AFE=∠CFD,由相似三角形判定和性质得![]() =1,即EF=DF,AF=CD,设CD=AF=x,则CE=8-x,由等腰直角三角形面积公式求得EF=DF=2
=1,即EF=DF,AF=CD,设CD=AF=x,则CE=8-x,由等腰直角三角形面积公式求得EF=DF=2![]() , 在Rt△EFD中,根据勾股定理得DE=2
, 在Rt△EFD中,根据勾股定理得DE=2![]() , 在Rt△EFD中,根据勾股定理列出方程解之得CD长.
, 在Rt△EFD中,根据勾股定理列出方程解之得CD长.
(2)设CD=x,则BD=8-x,根据等腰直角三角形性质和等量代换得∠AEF=∠BFD,由相似三角形判定和性质得![]() , 从而可得AF=8
, 从而可得AF=8![]() -
-![]() x,BF=
x,BF=![]() x,AE=2x,CE=8-2x,在Rt△CED中,根据勾股定理求得DE2=5x2-32x+64,由三角形面积公式得S△DEF=
x,AE=2x,CE=8-2x,在Rt△CED中,根据勾股定理求得DE2=5x2-32x+64,由三角形面积公式得S△DEF=![]() DE·DF=
DE·DF=![]() , 由二次函数性质可得△DEF的面积存在最小值及CD的长.
, 由二次函数性质可得△DEF的面积存在最小值及CD的长.
(1)解:①作FG⊥BC交BC于点G,如图:
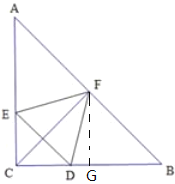
由题可得:CF垂直平分DE、AB,
设CE=CD=a,
∵∠ACB=90°,
∴DE=![]() a,
a,
∵△DEF是等边三角形,
∴DF=![]() a,
a,
∵FG⊥BC,CA=CB=8,
∴CG=BG=FG=4,DG=4-a,
在Rt△FGD中,
∴FD2=DG2+FG2 ,
即(![]() a)2=(4-a)2+42 ,
a)2=(4-a)2+42 ,
解得:a=4![]() -4,
-4,
∴DE=![]() a=
a=![]() ,
,
∴等边三角形△DEF边长为![]() ;
;
②如图2
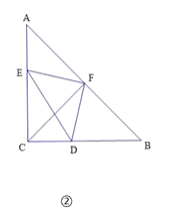
∵∠ACB=90°,CA=CB,点F时AB中点,
∴CF⊥AB,CF=AF,∠A=∠BCF=45°,
即∠AFE+∠EFC=90°,
∵∠EFD=90°,
即∠CFD+∠EFC=90°,
∴∠AFE=∠CFD,
在△AEF和△CDF中,
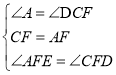
∴△AEF≌△CDF(ASA),
∴EF=DF,AF=CD,
设CD=AF=x,
∵AC=8,
∴CE=8-x,
又∵∠EFD=90°,
∴S△EFD=![]() ·EF·DF=10,
·EF·DF=10,
∴EF=DF=2![]() ,
,
在Rt△EFD中,
∴DE=![]() ,
,
在Rt△EFD中,
∵EC2+CD2=ED2 ,
∴(8-x)2+x2=40,
即(x-2)(x-6)=0,
解得:x=2,或x=6,
∴CD=2或6.
(2)解:设CD=x,则BD=8-x,
∵CA=CB=8,∠ACB=90°,
∴∠A=∠B=45°,AB=8![]() ,
,
又∵DE=DF,∠EDF=90°,
∴∠DEF=∠DFE=45°,EF=![]() DF,
DF,
∴∠AEF+∠AFE=135°,∠BFD+∠AFE=135°,
∴∠AEF=∠BFD,
∴△AFE∽△BDF,
∴![]() ,
,
∴AF=![]() BD=
BD=![]() (8-x)=8
(8-x)=8![]() -
-![]() x,BF=AB-AF=
x,BF=AB-AF=![]() x,
x,
∴AE=![]() BF=2x,CE=CA-AE=8-2x,
BF=2x,CE=CA-AE=8-2x,
在Rt△CED中,
∴DE2=CE2+CD2 ,
即DE2=x2+(8-2x)2=5x2-32x+64,
∴S△DEF=![]() ·DE·DF=
·DE·DF=![]() DE2,
DE2,
=![]() ,
,
=![]() ,
,
当且仅当![]() 时,△DEF的面积存在最小值,且最小值为
时,△DEF的面积存在最小值,且最小值为![]() .
.
∴CD=![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为![]() ,锅深
,锅深![]() ,锅盖高
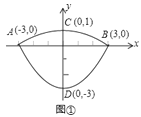
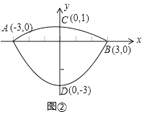
,锅盖高![]() (锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为
(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为![]() ,把锅盖纵断面的抛物线记为
,把锅盖纵断面的抛物线记为![]() .
.
![]() 求
求![]() 和
和![]() 的解析式;
的解析式;
![]() 如果炒菜锅时的水位高度是
如果炒菜锅时的水位高度是![]() ,求此时水面的直径;
,求此时水面的直径;
![]() 如果将一个底面直径为
如果将一个底面直径为![]() ,高度为
,高度为![]() 的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
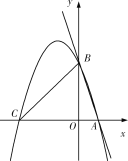
【题目】如图,已知直线y=-3x+c与x轴相交于点A(1,0),与y轴相交于点B,抛物线y=-x2+bx+c经过点A,B,与x轴的另一个交点是C.
(1)求抛物线的解析式;
(2)点P是对称轴的左侧抛物线上的一点,当S△PAB=2S△AOB时,求点P的坐标;
(3)连接BC,抛物线上是否存在点M,使∠MCB=∠ABO?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
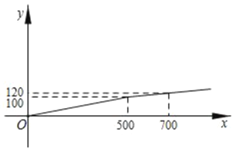
【题目】某校一课外小组准备进行“绿色环保”的宣传活动,需要印刷一批宣传单,学校附近有甲、乙两家印刷社,甲印刷社收费y(元)与印数x(张)的函数关系是:y=0.15x;乙印刷社收费y(元)与印数x(张)的函数关系如图所示:
(1)写出乙印刷社的收费y(元)与印数x(张)之间的函数关系式;
(2)若该小组在甲、乙两印刷社打印了相同数量的宣传单共用去70元,则共打印多少张宣传单?
(3)活动结束后,市民反映良好,兴趣小组决定再加印1500张宣传单,若在甲、乙印刷社中选一家,兴趣小组应选择哪家印刷社比较划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线 ![]() 相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
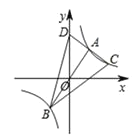
(1)k的值是________;
(2)若AD=AC,则△BCD的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC和△DBE均为等腰直角三角形,其中∠ABC=90°,∠DBE=90°.

(1)求证:AD=CE;
(2)求证:AD和CE垂直.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
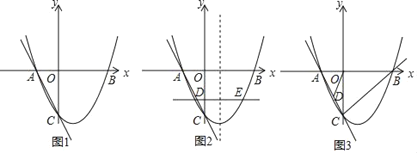
(1)求直线AC的解析式;
(2)如图2,点E(a,b)是对称轴右侧抛物线上一点,过点E垂直于y轴的直线与AC交于点D(m,n).点P是x轴上的一点,点Q是该抛物线对称轴上的一点,当a+m最大时,求点E的坐标,并直接写出EQ+PQ+![]() PB的最小值;
PB的最小值;
(3)如图3,在(2)的条件下,连结OD,将△AOD沿x轴翻折得到△AOM,再将△AOM沿射线CB的方向以每秒3个单位的速度沿平移,记平移后的△AOM为△A′O'M',同时抛物线以每秒1个单位的速度沿x轴正方向平移,点B的对应点为B'.△A'B'M'能否为等腰三角形?若能,请求出所有符合条件的点M'的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
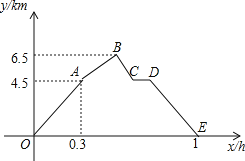
【题目】从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的地方,图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h;
③小明从甲地去乙地来回过程中,两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com