
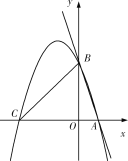
【题目】如图,已知直线y=-3x+c与x轴相交于点A(1,0),与y轴相交于点B,抛物线y=-x2+bx+c经过点A,B,与x轴的另一个交点是C.
(1)求抛物线的解析式;
(2)点P是对称轴的左侧抛物线上的一点,当S△PAB=2S△AOB时,求点P的坐标;
(3)连接BC,抛物线上是否存在点M,使∠MCB=∠ABO?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)y=-x2-2x+3;(2)P点的坐标为(-2,3);(3)存在点M,使∠MCB=∠ABO,点M的坐标为(![]() ,
,![]() )或(-1,4).
)或(-1,4).
【解析】
(1)先把A点坐标代入y=-3x+c求出得到B(0,3),然后利用待定系数法求抛物线解析式;
(2)连接OP,如图1,抛物线的对称轴为直线x=-1,设P(x,-x2-2x+3)(x<-1),由于S△PAB=S△POB+S△ABO-S△POA,S△PAB=2S△AOB,则S△POB-S△POA=S△ABO,讨论:当P点在x轴上方时,![]() ×3×(-x)-
×3×(-x)-![]() ×1×(-x2-2x+3)=
×1×(-x2-2x+3)=![]() ×1×3,当P点在x轴下方时,
×1×3,当P点在x轴下方时,![]() ×3×(-x)+
×3×(-x)+![]() ×1×(x2+2x-3)=
×1×(x2+2x-3)=![]() ×1×3,然后分别解方程求出x即可得到对应P点坐标;
×1×3,然后分别解方程求出x即可得到对应P点坐标;
(3)解方程-x2-2x+3=0得C(-3,0),则可判断△OBC为等腰直角三角形,讨论:当∠BCM在直线BC下方时,如图2,直线CM交y轴于D,作DE⊥BC于E,设D(0,t),表示出DE=BE=![]() (3-t),接着利用tan∠MCB=tan∠ABO得到
(3-t),接着利用tan∠MCB=tan∠ABO得到![]() ,所以3
,所以3![]() -
-![]() (3-t)=
(3-t)=![]() (3-t),解方程求出t得到D点坐标,接下来利用待定系数法确定直线CD的解析式为y=
(3-t),解方程求出t得到D点坐标,接下来利用待定系数法确定直线CD的解析式为y=![]() x+
x+![]() ,然后解方程组
,然后解方程组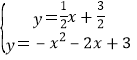 得此时M点坐标;当∠BCM在直线CB上方时,如图3,CM交直线AB于N,易得直线AB的解析式为y=-3x+3,设N(k,-3k+3),证明△ABC∽△ACN,利用相似比求出AN=
得此时M点坐标;当∠BCM在直线CB上方时,如图3,CM交直线AB于N,易得直线AB的解析式为y=-3x+3,设N(k,-3k+3),证明△ABC∽△ACN,利用相似比求出AN=![]() ,再利用两点间的距离公式得到(k-1)2+(-3k+3)2=(
,再利用两点间的距离公式得到(k-1)2+(-3k+3)2=(![]() )2,解方程求出t得N点坐标为(-
)2,解方程求出t得N点坐标为(-![]() ,
,![]() ),易得直线CN的解析式为y=2x+6,然后解方程组
),易得直线CN的解析式为y=2x+6,然后解方程组![]() 得此时M点坐标.
得此时M点坐标.
(1)把A(1,0)代入y=-3x+c得-3+c=0,解得c=3,则B(0,3),
把A(1,0),B(0,3)代入y=-x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=-x2-2x+3;
(2)连接OP,如图1,
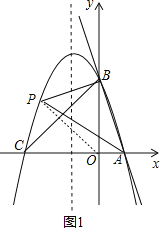
抛物线的对称轴为直线x=-![]() =-1,
=-1,
设P(x,-x2-2x+3)(x<-1),
S△PAB=S△POB+S△ABO-S△POA,
∵S△PAB=2S△AOB,
∴S△POB-S△POA=S△ABO,
当P点在x轴上方时,![]() ×3×(-x)-
×3×(-x)-![]() ×1×(-x2-2x+3)=
×1×(-x2-2x+3)=![]() ×1×3,解得x1=-2,x2=3(舍去),此时P点坐标为(-2,3);
×1×3,解得x1=-2,x2=3(舍去),此时P点坐标为(-2,3);
当P点在x轴下方时,![]() ×3×(-x)+
×3×(-x)+![]() ×1×(x2+2x-3)=
×1×(x2+2x-3)=![]() ×1×3,,解得x1=-2(舍去),x2=3(舍去),
×1×3,,解得x1=-2(舍去),x2=3(舍去),
综上所述,P点坐标为(-2,3);
(3)存在.
当y=0时,-x2-2x+3=0,解得x1=-1,x2=-3,则C(-3,0),
∵OC=OB=3,
∴△OBC为等腰直角三角形,
∴∠OBC=∠OCB=45°,BC=3![]() ,
,
当∠BCM在直线BC下方时,如图2,直线CM交y轴于D,作DE⊥BC于E,设D(0,t),
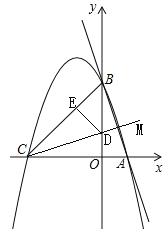
∵∠DBE=45°,
∴△BDE为等腰直角三角形,
∴DE=BE=![]() BD=
BD=![]() (3-t),
(3-t),
∵∠MCB=∠ABO,
∴tan∠MCB=tan∠ABO,
∴![]() ,即CE=3DE,
,即CE=3DE,
∴3![]() -
-![]() (3-t)=
(3-t)=![]() (3-t),解得t=
(3-t),解得t=![]() ,则D(0,
,则D(0,![]() ),
),
设直线CD的解析式为y=mx+n,
把C(-3,0),D(0,![]() )代入得
)代入得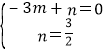 ,解得
,解得![]() ,
,
∴直线CD的解析式为y=![]() x+
x+![]() ,
,
解方程组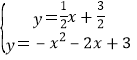 得
得![]() 或
或![]() ,此时M点坐标为(
,此时M点坐标为(![]() ,
,![]() );
);
当∠BCM在直线CB上方时,如图3,CM交直线AB于N,
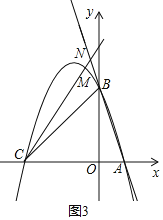
易得直线AB的解析式为y=-3x+3,AB=![]() ,AC=4
,AC=4
设N(k,-3k+3),
∵∠MCB=∠ABO,∠CBO=∠OCB,
∴∠NCA=∠ABC,
而∠BAC=∠CAN,
∴△ABC∽△ACN,
∴AB:AC=AC:AN,即![]() :4=4:AN,
:4=4:AN,
∴AN=![]() ,
,
∴(k-1)2+(-3k+3)2=(![]() )2,
)2,
整理得(k-1)2=![]() ,解得k1=
,解得k1=![]() (舍去),k2=-
(舍去),k2=-![]() ,
,
∴N点坐标为(-![]() ,
,![]() ),
),
易得直线CN的解析式为y=2x+6,
解方程组![]() ,得
,得![]() 或
或![]() ,此时M点坐标为(-1,4),
,此时M点坐标为(-1,4),
综上所述,满足条件的M点的坐标为(![]() ,
,![]() )或(-1,4).
)或(-1,4).
综上所述,存在点M,使∠MCB=∠ABO,点M的坐标为(![]() ,
,![]() )或(-1,4).
)或(-1,4).


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(1)求C点坐标,并判断b的正负性;
(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD与y轴交于点E,连接BC,
①若△BCE的面积为8,求二次函数的解析式;
②若△BCD为锐角三角形,请直接写出OA的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
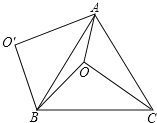
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O'的距离为8;③四边形AOBO'的面积为24+15![]() ; ④∠AOB=150°;⑤s△AOC+S△AOB=9
; ④∠AOB=150°;⑤s△AOC+S△AOB=9![]() +24,其中正确的结论是_____.
+24,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
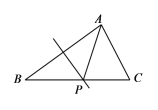
【题目】如图,在![]() 中,
中,![]() .
.
⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:![]() ;
;
⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
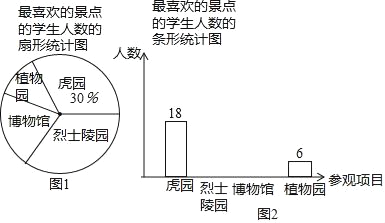
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
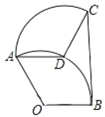
【题目】如图,将半径为1,圆心角为120°的扇形OAB绕点A逆时针旋转一个角度,使点O的对应点D落在弧AB上,点B的对应点为C,连接BC,则图中CD、BC和弧BD围成的封闭图形面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,有![]() ,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
,如图, △DEF的三个顶点D,E,F分别在△ABC的边BC,AC,AB上.
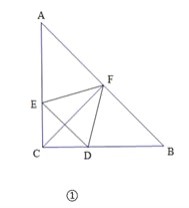
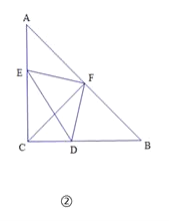
(1)已知点F是AB的中点.
①如图①,若△DEF是等边三角形,试直接写出正△DEF的边长;
②如图②,若![]() , △DEF 的面积为10,求CD的长;
, △DEF 的面积为10,求CD的长;
(2)若![]() ,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
,DF=DE, △DEF的面积是否存在最小值?若存在,求此时CD的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
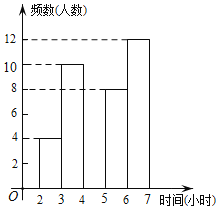
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com