练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知等腰△ABC中，AD⊥BC于点D，且AD=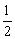BC，则△ABC底角的度数为(   )

    A．45°      B．75°      C．45°或75°      D．60°


    C.

    详解：根据题意画出图形，注意分别从∠BAC是顶角与∠BAC是底角去分析，然后利用等腰三角形与直角三角形的性质，即可求得答案：

    如图1：AB=AC，

    ∵AD⊥BC，∴BD=CD=BC，∠ADB=90°.

    ∵AD=BC，∴AD=BD. ∴∠B=45°.

    即此时△ABC底角的度数为45°.

    如图2，AC=BC，

    ∵AD⊥BC，∴∠ADC=90°.

    ∵AD=BC，∴AD=AC，∴∠C=30°.∴∠CAB=∠B=(1800－∠A)÷2=75°.

    即此时△ABC底角的度数为75°.

    综上所述，△ABC底角的度数为45°或75°.故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    九年级（1）班数学活动选出甲、乙两组各10名学生，进行趣味数学答题比赛，共10题，答对题数统计如表一：

    （表一）

    答对题数

    5

    6

    7

    8

    9

    10

    甲组

    1

    0

    1

    5

    2

    1

    乙组

    0

    0

    4

    3

    2

    1

    （表二）

    平均数

    众数

    中位数

    方差

    甲组

    8

    8

    8

    1.6

    乙

    8

    __________

    __________

    __________

    （1）根据表一中统计的数据，完成表二；

    （2）请你从平均数和方差的角度分析，哪组的成绩更好些？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的一元二次方程方程x2﹣2x+k=0有两个不相等的实数解，则k的范围是(     )

    A．k＞0 B．k＞1  C．k＜1 D．k≤1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个不透明的布袋里装有红、黄、绿三种颜色的球（除颜色不同，其它均无任何区别），其中红球2个，黄球1个，绿球1个．

    （1）求从袋中任意摸出一个球是红球的概率；

    （2）第一次从袋中任意摸出一个球，记下颜色后放回袋中，第二次再摸出一个球记下颜色，请用画树状图或列表的方法求两次都摸到红球的概率（两个红球分别记作红1、红2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，△ABC中，∠C=90°，学习等边三角形时，我们知道，如果∠A=30°，那么AB=2BC，由此我们猜想，如果AB=2BC，那么∠A=30°，请你利用轴对称变换，证明这个结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    题面：如图，△ABC的边BC的垂直平分线DE交△BAC的外角平分线AD于D，E为垂足，DF⊥AB于F，且AB＞AC，求证：BF=AC+AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    按要求分别写出一个大于9且小于10的无理数：

    (1)用一个平方根表示：                ；

    (2)用一个立方根表示：                ；

    (3)用含π的式子表示：                ；

    (4)用构造的方法表示：                ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是      ；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，Rt△ABO的顶点A是双曲线y1=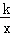与直线y2=﹣x﹣（k+1）在第二象限的交点．AB⊥x轴于B，且S△ABO=．

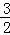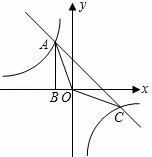    （1）求这两个函数的解析式；

    （2）求△AOC的面积．

    （3）直接写出使y1＞y2成立的x的取值范围

    查看答案和解析>>

    同步练习册答案