
【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针旋转________度得到;
(3)若BC=8,DE=6,求△AEF的面积.

【答案】(1)见解析 (2)A 90 (3)50
【解析】试题分析: (1)根据正方形的性质得AD=AB,∠D=∠ABC=90°,然后利用“SAS”易证得△ADE≌△ABF;
(2)由于△ADE≌△ABF得∠BAF=∠DAE,则∠BAF+∠BAE=90°,即∠FAE=90°,根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90度得到;
(3)先利用勾股定理可计算出AE=10,再根据△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90度得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
试题解析:
(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠ABF=∠ADE=90°.
∵DE=BF,
∴△ADE≌△ABF;
(2) ∵△ADE≌△ABF,
∴∠BAF=∠DAE,
而∠DAE+∠EAB=90°,
∴∠BAF+∠EAB=90°,即∠FAE=90°,
∴△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90度得到;
故答案为A.90;
(3)在Rt△ADE中,
∵AD=BC=8,DE=6,
∴AE=10.
由题意可知AF=AE=10,∠EAF=90°,
∴S△AEF=![]() AE·AF=50.
AE·AF=50.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
查看答案和解析>>
科目:初中数学 来源: 题型:
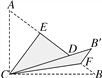
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4.将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )

A.20海里 B.40海里 C.![]() 海里 D.
海里 D.![]() 海里
海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com