
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).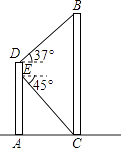
【答案】解:过点E、D分别作BC的垂线,交BC于点F、G.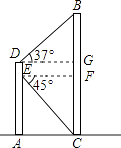
在Rt△EFC中,因为FC=AE=20,∠FEC=45°,
所以EF=20,
在Rt△DBG中,DG=EF=20,∠BDG=37°
因为tan∠BDG= ![]() ≈0.75,
≈0.75,
所以BG≈DG×0.75=20×0.75=15,
而GF=DE=5,
所以BC=BG+GF+FC=15+5+20=40.
答:大楼BC的高度是40米.
【解析】首先过点E、D分别作BC的垂线,交BC于点F、G,得两个直角三角形△EFC和△BDG,由已知大楼BC楼底C点的俯角为45°得出EF=FC=AE=20,DG=EF=20,再由直角三角形BDG,可求出BG,GF=DE=5,CO从而求出大楼的高度BC.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
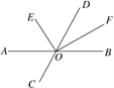
【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2mx+m2+m+1的图象与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图象关于x轴翻折,所得图象的顶点为D,若CD=8.求四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD.
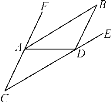
(1)判断∠FAB与∠C的大小关系,请说明理由;
(2)若∠C=35°,AB是∠FAD的平分线.
①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
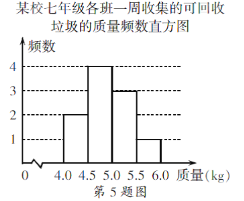
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
查看答案和解析>>
科目:初中数学 来源: 题型:
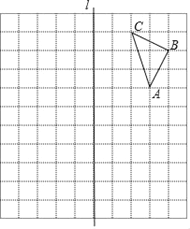
【题目】如图,直线l与△ABC在边长为1个单位长度的小正方形网格中,点A,B,C都为网格线的交点.
(1)请画出△ABC关于直线l对称的△A1B1C1(点A,B,C的对称点分别为A1,B1,C1).
(2)请画出将线段AC向左平移3个单位,再向下平移5个单位得到的线段A2C2(点A,C的对应点分别为A2,C2),再以A2C2为斜边画一个等腰直角三角形A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
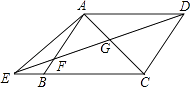
【题目】如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 ![]() =
= ![]() .
. 
(1)求证:AB∥CD;
(2)如果AD2=DGDE,求证: ![]() =
= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com