
【题目】已知二次函数y=x2﹣2mx+m2+m+1的图象与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图象关于x轴翻折,所得图象的顶点为D,若CD=8.求四边形ACBD的面积.
【答案】
(1)解:∵二次函数图象与x轴有两个交点,
∴△=4m2﹣4(m2+m+1)=﹣4m﹣4>0,
∴m<﹣1;
(2)解:y=x2﹣2m x+m2+m+1=(x﹣m) 2+m+1,
∵CD=8,
∴m+1=﹣4,解得m=﹣5,
∴y=x2+10 x+21,
令y=0,x2+10 x+21=0,解得x1=﹣3,x2=﹣7,则A(﹣3,0),B(﹣7,0)
∴AB=4,
∴S四边形ACBD=2× ![]() ×4×4=16.
×4×4=16.
【解析】(1)根据判别式的意义得到△=4m2﹣4(m2+m+1)=﹣4m﹣4>0,然后解不等式即可;(2)先配方得到y=(x﹣m) 2+m+1,则顶点的纵坐标为m+1,利用C点和D点关于x轴对称得到m+1=﹣4,解得m=﹣5,所以y=x2+10 x+21,然后解方程x2+10 x+21=0得到A(﹣3,0),B(﹣7,0),再利用三角形面积公式计算四边形ACBD的面积.
【考点精析】解答此题的关键在于理解二次函数图象的平移的相关知识,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.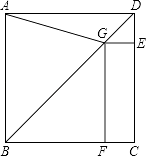
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
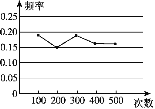
A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 掷一个质地均匀的正方体骰子,落地时面朝上的点数是6
C. 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上
D. 用2,3,4三个数字随机排成一个三位数,排出的数是偶数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的日历表,在此目历表上可以用一个“十”字圈出5个数.
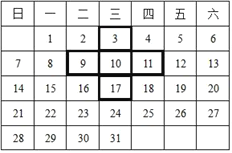
(1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系?
(2)照此方法,任意圈出的5个数是否都具有这样的数量关系?请通过整式的运算说明理由.
(3)用(2)的结论说明圈出的5个数的和能否等于125?
查看答案和解析>>
科目:初中数学 来源: 题型:
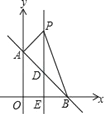
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).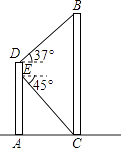
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
①s△OEB=s△ODB , ②BD=4AD,③连接MD,S△ODM=2S△OCE , ④连接ED,则△BED∽△BCA.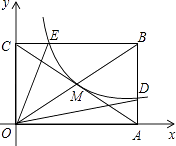
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com